题目内容
7.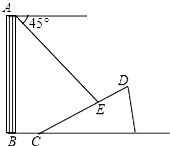 如图,一楼房AB后有一假山,山坡斜面CD与水平面夹角为30°,坡面上点E处有一亭子,测得假山坡脚C与楼房水平距离BC=10米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.求楼房AB的高(结果保留根号).
如图,一楼房AB后有一假山,山坡斜面CD与水平面夹角为30°,坡面上点E处有一亭子,测得假山坡脚C与楼房水平距离BC=10米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.求楼房AB的高(结果保留根号).
分析 过点E作EF⊥BC于点F.在Rt△CEF中,求出CF,然后根据勾股定理解答即可.
解答 解:过点E作EF⊥BC于点F.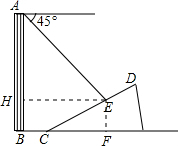
在Rt△CEF中,CE=20,∠ECF=30°
∴EF=10,
CF=$\sqrt{3}$EF=10$\sqrt{3}$(米),
过点E作EH⊥AB于点H.则HE=BF,BH=EF.
在Rt△AHE中,∠HAE=45°,
∴AH=HE,
又∵BC=10米,∴HE=(10+10$\sqrt{3}$)米,
∴AB=AH+BH=10+10$\sqrt{3}$+10=20+10$\sqrt{3}$(米)
答:楼房AB的高为(20+10$\sqrt{3}$) 米.
点评 本题考查了解直角三角形的应用--仰角俯角问题、坡度坡角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
17.为执行中央“节能减排,美化环境,建设美丽新农村”的国策,我市某村计划建造A、B两种型号的沼气池共20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积、使用农户数及造价见下表:
已知可供建造沼气池的占地面积不超过370m2,该村农户共有498户.
(1)满足条件的方案共有哪几种?写出解答过程.
(2)通过计算判断,哪种建造方案最省钱?造价最低是多少万元?
| 型号 | 占地面积(m2/个) | 使用农户数(户/个) | 造价(万元/个) |
| A | 15 | 18 | 2 |
| B | 20 | 30 | 3 |
(1)满足条件的方案共有哪几种?写出解答过程.
(2)通过计算判断,哪种建造方案最省钱?造价最低是多少万元?
15. 一个反比例函数在第二象限的图象如图所示,点A是图象上任意一点,AM⊥x轴,垂足为M,O是原点,如果△AOM的面积是3,求这个反比例函数的解析式是( )
一个反比例函数在第二象限的图象如图所示,点A是图象上任意一点,AM⊥x轴,垂足为M,O是原点,如果△AOM的面积是3,求这个反比例函数的解析式是( )
 一个反比例函数在第二象限的图象如图所示,点A是图象上任意一点,AM⊥x轴,垂足为M,O是原点,如果△AOM的面积是3,求这个反比例函数的解析式是( )
一个反比例函数在第二象限的图象如图所示,点A是图象上任意一点,AM⊥x轴,垂足为M,O是原点,如果△AOM的面积是3,求这个反比例函数的解析式是( )| A. | y=-$\frac{3}{x}$ | B. | y=$\frac{3}{x}$ | C. | y=$\frac{6}{x}$ | D. | y=-$\frac{6}{x}$ |
12.81的算术平方根是( )
| A. | 9 | B. | ±9 | C. | 3 | D. | ±3 |
19.有一组数据:1,3,4,5,5,则这组数据的平均数,众数,中位数分别是( )
| A. | 3.6,5,5 | B. | 5,5,5 | C. | 3.6,5,4 | D. | 3.6,4,5 |
16.小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为95分、80分、90分,若依次按照60%、30%、10%确定成绩,则小王的成绩是( )
| A. | 85.5分 | B. | 90分 | C. | 92分 | D. | 265分 |
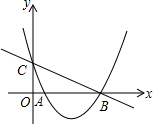 如图,已知抛物线y=ax2-5ax+2(a≠0)与y轴交于点C,与x轴交于点A(1,0)和点B.
如图,已知抛物线y=ax2-5ax+2(a≠0)与y轴交于点C,与x轴交于点A(1,0)和点B.