Question

15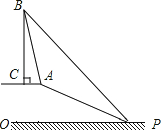．已知，如图，在笔山银子岩坡顶A处的同一水平面上有一座移动信号发射塔BC，
笔山职中数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°，然后他们沿着坡度为1：2.4的斜坡AP攀行了26米，在坡顶A处又测得该塔的塔顶B的仰角为76°．求：
（1）坡顶A到地面PO的距离；
（2）移动信号发射塔BC的高度（结果精确到1米）．
（参考数据：sin76°≈0.97，cos76°≈0.24，tan76°≈4.01）

Answer 1

分析 （1）过点A作AH⊥PQ，垂足为点H，利用斜坡AP的坡度为1：2.4，得出AH，PH，AP的关系求出即可；
（2）利用矩形性质求出设BC=x，则x+10=24+DH，再利用tan76°=$\frac{BC}{AC}$，求出即可．

解答 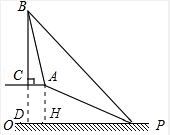解：（1）过点A作AH⊥PO，垂足为点H，
∵斜坡AP的坡度为1：2.4，
∴$\frac{AH}{PH}$=$\frac{5}{12}$，
设AH=5k，则PH=12k，由勾股定理，得AP=13k，
∴13k=26，
解得k=2，∴AH=10，
答：坡顶A到地面PQ的距离为10米．

（2）延长BC交PO于点D，
∵BC⊥AC，AC∥PO，∴BD⊥PO，
∴四边形AHDC是矩形，CD=AH=10，AC=DH，
∵∠BPD=45°，∴PD=BD，
设BC=x，则x+10=24+DH，
∴AC=DH=x-14，
在Rt△ABC中，tan76°=$\frac{BC}{AC}$，即$\frac{x}{x-14}$≈4.01．
解得x≈19．
答：移动信号发射塔BC的高度约为19米．

点评 此题主要考查了坡度问题以及仰角的应用，根据已知在直角三角形中得出各边长度是解题关键．