题目内容
10.数学复习课上,王老师出示了如框中的题目:
题目中的黑色矩形框部分是一段被墨水污染了无法辨认的文字
(1)根据已知和结论中现有的信息,你能否求出题中直线的解析式?若能,请写出求解过程;若不能,请说明理由
(2)请你根据已有的信息,在原题中的矩形框中,填加一个适当的条件,把原题补充完整,你填加的这个条件是?
分析 (1)把点M的坐标代入双曲线的解析式中得到关于b的方程,解该方程即可求出b的值,从而求得M的坐标,代入直线的解析式即可求得k的值,从而求得一次函数的解析式;
(2)根据(1)中所求的函数解析式可写出图象上另一个点的坐标,答案不唯一.填加的条件只要能确保b=-2就可以.
解答 解:(1)能.
由结论中的点M一定在双曲线y=$\frac{2b}{x}$上,得-b=$\frac{2b}{b}$,则b=-2,
∴M(-2,2),
∴2=-2k-2,解得k=-2,
∴直线的解析式为y=-2x-2.
(2)答案不唯一,如;直线y=kx+b经过点N(1,-4)等等.
点评 主要考查了用待定系数法求一次函数解析式.要熟练待定系数法并会灵活运用.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
20. 如图,若∠1+∠2=180°,则( )
如图,若∠1+∠2=180°,则( )
 如图,若∠1+∠2=180°,则( )
如图,若∠1+∠2=180°,则( )| A. | c∥d | B. | a∥b | C. | c∥d且a∥b | D. | ∠3=∠2 |
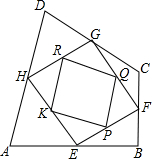 如图,ABCD是校内一块四边形空地,学校在征集对这块空地种花草的设计中选定了如下方案:把这块四边形空地分成九块,种植三种不同品种的花草,其中E,F,G,H分别是AB,BC,CD,DA的中点,P,Q,R,K分别是EF,FG,GH,HE的中点,现在要在四边形PQRK中种上红色的花,在△PFQ,△QGR,△RHK,△KEP中种上黄色的花,在△HAE,△EBF,△FCG,△GDH中种上紫色的花.已知红,黄,紫三种花的单价分别是8元/m2,10元/m2,12元/m2,而种红花共用去120元,请用学过的数学知识计算种满四边形ABCD这块空地的花需要多少元?
如图,ABCD是校内一块四边形空地,学校在征集对这块空地种花草的设计中选定了如下方案:把这块四边形空地分成九块,种植三种不同品种的花草,其中E,F,G,H分别是AB,BC,CD,DA的中点,P,Q,R,K分别是EF,FG,GH,HE的中点,现在要在四边形PQRK中种上红色的花,在△PFQ,△QGR,△RHK,△KEP中种上黄色的花,在△HAE,△EBF,△FCG,△GDH中种上紫色的花.已知红,黄,紫三种花的单价分别是8元/m2,10元/m2,12元/m2,而种红花共用去120元,请用学过的数学知识计算种满四边形ABCD这块空地的花需要多少元?
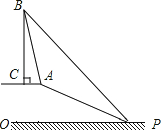 已知,如图,在笔山银子岩坡顶A处的同一水平面上有一座移动信号发射塔BC,
已知,如图,在笔山银子岩坡顶A处的同一水平面上有一座移动信号发射塔BC,