题目内容
3.已知直线y=-$\frac{1}{2}$kx+3与y=-$\frac{1}{m}$x+2.(1)如果两直线相交于($\frac{3}{2}$,-$\frac{3}{2}$),求km的值.
(2)如果两直线平行,求km的值.
分析 (1)根据两直线相交的问题,把($\frac{3}{2}$,-$\frac{3}{2}$)分别代入两直线解析式求出k和m的值,然后计算km;
(2)根据两直线平行的问题得到-$\frac{1}{2}$k=-$\frac{1}{m}$,然后利用等式的性质即可得到km的值.
解答 解:(1)把($\frac{3}{2}$,-$\frac{3}{2}$)分别代入y=-$\frac{1}{2}$kx+3与y=-$\frac{1}{m}$x+2得-$\frac{1}{2}$•k•$\frac{3}{2}$+3=-$\frac{3}{2}$,-$\frac{1}{m}$•$\frac{3}{2}$+2=-$\frac{3}{2}$,
解得k=6,m=$\frac{3}{7}$,
所以km=6×$\frac{3}{7}$=$\frac{18}{7}$;
(2)因为直线y=-$\frac{1}{2}$kx+3与y=-$\frac{1}{m}$x+2平行,
所以-$\frac{1}{2}$k=-$\frac{1}{m}$,
所以km=2.
点评 本题考查了两条直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
13.设a=$\sqrt{17}$-$\frac{1}{2}$,则a在两个相邻整数之间,这两个整数是( )
| A. | 4和5 | B. | 3和4 | C. | 2和3 | D. | 1和2 |
14.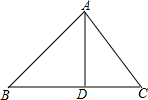 如图,AB⊥AC,AD⊥BC,如果AB=4cm,AC=3cm,AD=2.4cm,那么点C到直线AB的距离为( )
如图,AB⊥AC,AD⊥BC,如果AB=4cm,AC=3cm,AD=2.4cm,那么点C到直线AB的距离为( )
 如图,AB⊥AC,AD⊥BC,如果AB=4cm,AC=3cm,AD=2.4cm,那么点C到直线AB的距离为( )
如图,AB⊥AC,AD⊥BC,如果AB=4cm,AC=3cm,AD=2.4cm,那么点C到直线AB的距离为( )| A. | 3cm | B. | 4cm | C. | 2.4cm | D. | 无法确定 |
8.下列各式中,与(2-$\sqrt{3}$)的积为有理数的是( )
| A. | 2$\sqrt{3}$ | B. | 2-$\sqrt{3}$ | C. | -2+$\sqrt{3}$ | D. | 2+$\sqrt{3}$ |
 已知:如图,点B,E,C,F在一条直线上,AB∥DE,∠A=∠D,AC⊥BF,AC与DE相交于点M,对DF⊥BF说明理由.
已知:如图,点B,E,C,F在一条直线上,AB∥DE,∠A=∠D,AC⊥BF,AC与DE相交于点M,对DF⊥BF说明理由.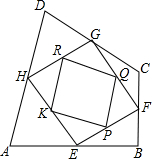 如图,ABCD是校内一块四边形空地,学校在征集对这块空地种花草的设计中选定了如下方案:把这块四边形空地分成九块,种植三种不同品种的花草,其中E,F,G,H分别是AB,BC,CD,DA的中点,P,Q,R,K分别是EF,FG,GH,HE的中点,现在要在四边形PQRK中种上红色的花,在△PFQ,△QGR,△RHK,△KEP中种上黄色的花,在△HAE,△EBF,△FCG,△GDH中种上紫色的花.已知红,黄,紫三种花的单价分别是8元/m2,10元/m2,12元/m2,而种红花共用去120元,请用学过的数学知识计算种满四边形ABCD这块空地的花需要多少元?
如图,ABCD是校内一块四边形空地,学校在征集对这块空地种花草的设计中选定了如下方案:把这块四边形空地分成九块,种植三种不同品种的花草,其中E,F,G,H分别是AB,BC,CD,DA的中点,P,Q,R,K分别是EF,FG,GH,HE的中点,现在要在四边形PQRK中种上红色的花,在△PFQ,△QGR,△RHK,△KEP中种上黄色的花,在△HAE,△EBF,△FCG,△GDH中种上紫色的花.已知红,黄,紫三种花的单价分别是8元/m2,10元/m2,12元/m2,而种红花共用去120元,请用学过的数学知识计算种满四边形ABCD这块空地的花需要多少元?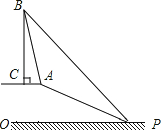 已知,如图,在笔山银子岩坡顶A处的同一水平面上有一座移动信号发射塔BC,
已知,如图,在笔山银子岩坡顶A处的同一水平面上有一座移动信号发射塔BC, 已知实数a、b、c(在数轴上的位置如图所示),化简:|2a+2|-|c-b|-|a+b+2|.
已知实数a、b、c(在数轴上的位置如图所示),化简:|2a+2|-|c-b|-|a+b+2|.