题目内容
17.(1)(-a)2•(a2)2÷a3;(2)-4a(2a2+3a-1)
(3)(-1)2006+(-$\frac{1}{2}$)-2-(3.14-π)0+(-2)3
(4)(2x-3y)2-(y+3x)(3x-y)
(5)(2x-y+1)(2x+y-1)
(6)用简便方法计算:1232-121×119
(7)先化简,再求值:(2x+3)(2x-3)-2x(x-1)-2(x-1)2,其中x=-1.
分析 (1)原式利用积的乘方与幂的乘方运算法则计算,即可得到结果;
(2)原式利用单项式乘以多项式法则计算即可得到结果;
(3)原式利用乘方的意义,零指数幂、负整数指数幂法则计算即可得到结果;
(4)原式利用完全平方公式,平方差公式计算即可得到结果;
(5)原式利用平方差公式及完全平方公式化简即可得到结果;
(6)原式变形后,利用平方差公式计算即可得到结果;
(7)原式利用平方差公式,完全平方公式,以及单项式乘以多项式法则计算得到最简结果,把x的值代入计算即可求出值.
解答 解:(1)原式=a2•a4÷a3=a3;
(2)原式=-8a3-12a2+4a;
(3)原式=1+4-1-8=-4;
(4)原式=4x2-12xy+9y2-9x2+y2=-5x2-12xy+10y2;
(5)原式=(2x2)2-(y-1)2=4x2-y2+2y-1;
(6)原式=1232-(120-1)×(120+1)=1232-1202+1=253×3+1=760;
(7)原式=4x2-9-2x2+2x-2x2+4x-2=6x-11,
当x=-1时,原式=-6-11=-17.
点评 此题考查了整式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
12.若方程组$\left\{\begin{array}{l}{2a-3b=13}\\{3a+5b=30}\end{array}\right.$的解是$\left\{\begin{array}{l}{a=8.3}\\{b=1.2}\end{array}\right.$,则方程组$\left\{\begin{array}{l}{2(x+2)-3(y-1)=13}\\{3(x+2)+5(y-1)=30}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=8.3}\\{y=1.2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=10.3}\\{y=1.2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=6.3}\\{y=2.2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=10.3}\\{y=0.2}\end{array}\right.$ |
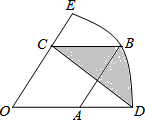 如图,在扇形EOD中,OD=3,菱形OABC的顶点A、B、C分别在OD、$\widehat{DE}$和OE上,OA=$\sqrt{3}$,连接CD,则阴影部分的面积为$\frac{3π-9+3\sqrt{3}}{4}$.
如图,在扇形EOD中,OD=3,菱形OABC的顶点A、B、C分别在OD、$\widehat{DE}$和OE上,OA=$\sqrt{3}$,连接CD,则阴影部分的面积为$\frac{3π-9+3\sqrt{3}}{4}$.

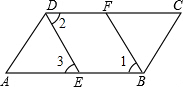 如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,DE∥FB.求证:AB∥DC.
如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,DE∥FB.求证:AB∥DC.