题目内容
5.已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B的左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“关联”抛物线,直线AC′为抛物线p的“关联”直线.若一条抛物线的“关联”抛物线和“关联”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为y=x2-2x-3.分析 先求出y=x2+2x+1和y=2x+2的交点C′的坐标为(1,4),再求出“关联”抛物线y=x2+2x+1的顶点A坐标(-1,0),接着利用点C和点C′关于x轴对称得到C(1,-4),则可设顶点式y=a(x-1)2-4,然后把A点坐标代入求出a的值即可得到原抛物线解析式.
解答 解:∵y=x2+2x+1=(x+1)2,
∴A点坐标为(-1,0),
解方程组$\left\{\begin{array}{l}{y={x}^{2}+2x+1}\\{y=2x+2}\end{array}\right.$,
得$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$,
∴点C′的坐标为(1,4),
∵点C和点C′关于x轴对称,
∴C(1,-4),
设原抛物线解析式为y=a(x-1)2-4,
把A(-1,0)代入得4a-4=0,解得a=1,
∴原抛物线解析式为y=(x-1)2-4=x2-2x-3.
故答案为:y=x2-2x-3.
点评 本题考查了二次函数与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.△=b2-4ac决定抛物线与x轴的交点个数,△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
18.在($\frac{2}{3}$)2,($\frac{3}{4}$)-2,($\frac{6}{5}$)2,($\frac{6}{7}$)0这四个数中,最小的是( )
| A. | ($\frac{2}{3}$)2 | B. | ($\frac{3}{4}$)-2 | C. | ($\frac{6}{5}$)2 | D. | ($\frac{6}{7}$)0 |
13.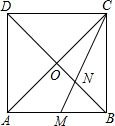 如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=2,则正方形的边长为( )
如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=2,则正方形的边长为( )
 如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=2,则正方形的边长为( )
如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=2,则正方形的边长为( )| A. | 4 | B. | 3 | C. | 2+$\sqrt{2}$ | D. | $\sqrt{2}+1$ |
15.已知抛物线y=2x2-8x+6与x轴相交于点A、B(点A在点B的左边),与y轴交于点C,BC的中点为M,点B关于y轴的对称点为N,则MN的长度等于( )
| A. | $\frac{3\sqrt{13}}{2}$ | B. | $\frac{\sqrt{119}}{2}$ | C. | $\frac{\sqrt{110}}{2}$ | D. | 6 |
 如图,抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.
如图,抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.