题目内容
6.已知关于x、y的方程组$\left\{\begin{array}{l}{x+3y=4-a}\\{x-5y=3a}\end{array}\right.$,给出下列结论:①$\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$是方程组的解;
②无论a取何值,x,y的值都不可能互为相反数;
③当a=1时,方程组的解也是方程x+y=4-a的解;
④x,y的都为自然数的解有4对.
其中正确的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①将x=5,y=-1代入检验即可做出判断;
②将x和y分别用a表示出来,然后求出x+y=3来判断;
③将a=1代入方程组求出方程组的解,代入方程中检验即可;
④有x+y=3得到x、y都为自然数的解有4对.
解答 解:①将x=5,y=-1代入方程组得:$\left\{\begin{array}{l}{5-3=4-a①}\\{5+5=3a②}\end{array}\right.$,
由①得a=2,由②得a=$\frac{10}{3}$,故①不正确.
②解方程$\left\{\begin{array}{l}{x+3y=4-a①}\\{x-5y=3a②}\end{array}\right.$
①-②得:8y=4-4a
解得:y=$\frac{1-a}{2}$
将y的值代入①得:x=$\frac{a+5}{2}$,
所以x+y=3,故无论a取何值,x、y的值都不可能互为相反数,故②正确.
③将a=1代入方程组得:$\left\{\begin{array}{l}{x+3y=3}\\{x-5y=3}\end{array}\right.$
解此方程得:$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$
将x=3,y=0代入方程x+y=3,方程左边=3=右边,是方程的解,故③正确.
④因为x+y=3,所以x、y都为自然数的解有$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$,$\left\{\begin{array}{l}{x=0}\\{y=3}\end{array}\right.$,$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,.故④正确.
则正确的选项有②③④,
故选:C.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案| A. | $\frac{3\sqrt{13}}{2}$ | B. | $\frac{\sqrt{119}}{2}$ | C. | $\frac{\sqrt{110}}{2}$ | D. | 6 |
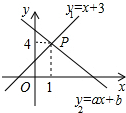 如图,一次函数y1=x+3与y2=ax+b的图象相交于点P(1,4),则关于x的不等式x+3≤ax+b的解集是( )
如图,一次函数y1=x+3与y2=ax+b的图象相交于点P(1,4),则关于x的不等式x+3≤ax+b的解集是( )| A. | x≥4 | B. | x≤4 | C. | x≥1 | D. | x≤1 |
| A. | (b-2,-a) | B. | (b+2,-a) | C. | (-a+2,-b) | D. | (-a-2,-b) |