题目内容
12.若方程组$\left\{\begin{array}{l}{2a-3b=13}\\{3a+5b=30}\end{array}\right.$的解是$\left\{\begin{array}{l}{a=8.3}\\{b=1.2}\end{array}\right.$,则方程组$\left\{\begin{array}{l}{2(x+2)-3(y-1)=13}\\{3(x+2)+5(y-1)=30}\end{array}\right.$的解是( )| A. | $\left\{\begin{array}{l}{x=8.3}\\{y=1.2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=10.3}\\{y=1.2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=6.3}\\{y=2.2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=10.3}\\{y=0.2}\end{array}\right.$ |
分析 根据加减法,可得(x+2)、(y-1)的解,再根据解方程,可得答案.
解答 解:∵方程组$\left\{\begin{array}{l}{2a-3b=13}\\{3a+5b=30}\end{array}\right.$的解是$\left\{\begin{array}{l}{a=8.3}\\{b=1.2}\end{array}\right.$,
∴方程组$\left\{\begin{array}{l}{2(x+2)-3(y-1)=13}\\{3(x+2)+5(y-1)=30}\end{array}\right.$中$\left\{\begin{array}{l}{x+2=8.3}\\{y-1=1.2}\end{array}\right.$
∴$\left\{\begin{array}{l}{x=6.3}\\{y=2.2}\end{array}\right.$
故选:C.
点评 本题考查了二元一次方程组的解,解决本题的关键是先求(x+2)、(y-1)的解,再求x、y的值.

练习册系列答案
相关题目
5. 如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,图中与△DEF全等的三角形有( )
如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,图中与△DEF全等的三角形有( )
 如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,图中与△DEF全等的三角形有( )
如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,图中与△DEF全等的三角形有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
7.如果不等式组$\left\{\begin{array}{l}{x<5}\\{x<m}\end{array}\right.$的解集为x<5,那么m的取值范围是( )
| A. | m>5 | B. | m≥5 | C. | m<5 | D. | m≤5 |
4.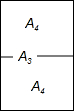 复印纸的型号有A0、A1、A2、A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )
复印纸的型号有A0、A1、A2、A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )
 复印纸的型号有A0、A1、A2、A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )
复印纸的型号有A0、A1、A2、A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )| A. | 2:1 | B. | $\sqrt{2}$:1 | C. | $\sqrt{3}$:1 | D. | 3:1 |
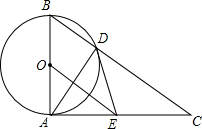 如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.
如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA. 已知二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-1,-5.2)及部分图象(如图),由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是x1,x2,若x1=1.3,则x2的值为( )
已知二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-1,-5.2)及部分图象(如图),由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是x1,x2,若x1=1.3,则x2的值为( )