Question

6．已知⊙O的半径为4，BC为⊙O的弦，∠OBC=60°，P是射线AO上的一动点，连结CP．
（1）当点P运动到如图1所示的位置时，S_△PBC=4$\sqrt{3}$，求证：CP是⊙O的切线；
（2）如图2，当点P在直径AB上运动时，CP的延长线与⊙O相交于点Q，试问PB为何值时，△CBQ是等腰三角形？

Answer 1

分析 （1）连接OC，过点C作CE⊥AB于点E，由“∠OBC=60°，OB=OC”可知△OBC是等边三角形，结合等边三角形的性质可求出CE、OE的长度，由△PBC的面积为4$\sqrt{3}$结合三角形的面积公式可算出BP的长度，由勾股定理即可求出PC的长度，在△OCP中知道三边长度，由三边长度满足OP²=OC²+PC²，可得出结论．
（2）△CBQ是等腰三角形分两种情况，通过画图找出两种情况．①过点C作CP′⊥OB，垂足为P′，延长CP′交⊙O于点Q′，结合△OBC是等边三角形即可得出P′B的长度；②过O作OD⊥BC与点D，延长DO交⊙O于点Q″，连接CQ″交AB于点P″，结合垂径定理可得出此时△CBQ″是等腰三角形，根据边角关系可找出∠P″CP′=45°，即得出△CP′P″是等腰直角三角形，通过解直角三角形即可得出结论．

解答 （1）证明：连接OC，过点C作CE⊥AB于点E，如图1所示．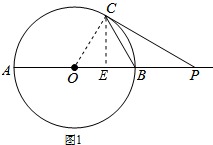

∵∠OBC=60°，OB=OC，
∴△OBC是等边三角形，
∴∠COE=60°，
∴CE=OC•sin∠COE=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$，OE=OC•cos∠COE=4×$\frac{1}{2}$=2．
∵S_△PBC=$\frac{1}{2}$BP•CE=4$\sqrt{3}$，
∴BP=4，
∴EP=OB-OE+BP=4-2+4=6．
由勾股定理得：PC=$\sqrt{C{E}^{2}+E{P}^{2}}$=4$\sqrt{3}$．
在△OCP中，OC=4，PC=4$\sqrt{3}$，OP=OB+BP=8，
满足OP²=OC²+PC²，
∴∠OCP=90°，
∴CP是⊙O的切线．
（2）解：△CBQ是等腰三角形分两种情况，具体情形如图2所示．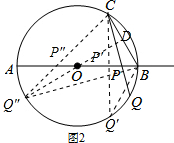

①过点C作CP′⊥OB，垂足为P′，延长CP′交⊙O于点Q′，
∵AB是⊙O的直径，
∴$\widehat{BC}=\widehat{BQ′}$，
∴BC=BQ′，
∴△CBQ′是等腰三角形．
由（1）可知△OBC是等边三角形，
∴P′B=BC•cos60°=4×$\frac{1}{2}$=2；
②过O作OD⊥BC与点D，延长DO交⊙O于点Q″，连接CQ″交AB于点P″，
∵O是圆心，
∴DQ″是BC的垂直平分线，
∴CQ″=BQ″，
∴△CBQ″是等腰三角形．
∵∠COB=60°，
∴∠CQ″B=$\frac{1}{2}$∠COB=30°．
∵DQ″平分∠CQ″B，OC=OQ″，
∴∠CQ″O=∠OCQ″=15°．
∵△OBC是等边三角形，CP′⊥OB，
∴∠OCP′=$\frac{1}{2}$∠OCB=30°，
∴∠P″CP′=∠P′CO+∠OCQ″=30°+15°=45°，
∴△CP′P″是等腰直角三角形，
∴P′P″=CP′=2$\sqrt{3}$，
∴P″B=P′P″+P′B=2$\sqrt{3}$+2．
综上可知：当PB为2或2$\sqrt{3}$+2时，△CBQ是等腰三角形．

点评 本题考查了切线的判定、等腰三角形的判定、等边三角形的性质、垂径定理以及三角形的面积公式，解题的关键是：（1）验证△OCP三边是否满足OP²=OC²+PC²；（2）寻找到满足△CBQ是等腰三角形的两种情况下的P点的位置．本题属于中档题，（1）难度不大；（2）中第一种情况很简单，可第二种情况的寻找比较麻烦，给同学们造成了很大的干扰．解决该题型题目时，根据边角关系找垂直是关键．