题目内容
在等腰三角形中,一边上的高为
,这条高与底边的夹角为60°,则此三角形面积为( )
| 3 |
| A、2 | ||||
B、2
| ||||
C、
| ||||
D、
|
考点:勾股定理,等腰三角形的性质,含30度角的直角三角形
专题:
分析:根据等腰三角形性质求出∠C=∠ABC,求出∠C=∠ABC=30°,解直角三角形求出AB、根据三角形面积公式求出即可.
解答: 解:∵AB=AC,
解:∵AB=AC,
∴∠C=∠ABC,
如图所示,根据题意得:∠DBC=60°,∠D=90°,
∴∠ABC=∠C=30°,
∴∠DBA=60°-30°=30°,
∵BD=
,
∴AD=1,AB=2=AC,
∴△ABC的面积S=
×AC×BD=
×2×
=
,
故选D.
 解:∵AB=AC,
解:∵AB=AC,∴∠C=∠ABC,
如图所示,根据题意得:∠DBC=60°,∠D=90°,
∴∠ABC=∠C=30°,
∴∠DBA=60°-30°=30°,
∵BD=
| 3 |
∴AD=1,AB=2=AC,
∴△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故选D.
点评:本题考查了三角形内角和定理,等腰三角形的性质,解直角三角形的应用,解此题的关键是求出腰AC的长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
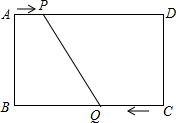 如图,在长方形ABCD中,AD=BC=12cm,AB=DC=8cm,动点P从点A出发沿AD向点D运动,速度是1cm/s,动点Q从点C出发沿CB向点B运动,当到达点B后继续沿BA向点A运动,速度是3cm/s,P,Q两点同时出发,从两点出发时开始计时,设运动的时间是t(s).当点Q在线段CB上运动时,t为何值时,PD=CQ?
如图,在长方形ABCD中,AD=BC=12cm,AB=DC=8cm,动点P从点A出发沿AD向点D运动,速度是1cm/s,动点Q从点C出发沿CB向点B运动,当到达点B后继续沿BA向点A运动,速度是3cm/s,P,Q两点同时出发,从两点出发时开始计时,设运动的时间是t(s).当点Q在线段CB上运动时,t为何值时,PD=CQ?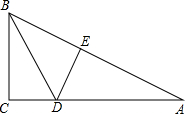 已知,如图,△ABC中,∠C=90°,AB=10,AC=8,BD为∠ABC的角平分线交AC于D,过点D作DE垂直AB于点E,
已知,如图,△ABC中,∠C=90°,AB=10,AC=8,BD为∠ABC的角平分线交AC于D,过点D作DE垂直AB于点E,