题目内容
已知直线y=mx与双曲线y=-
交于(x1,y1)、(x2,y2)两点,求-9x1y2+3x2y1的值.
| 5 |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:首先解两个解析式组成的方程组求得x1、x2以及对应的y1和y2的值,然后代入求解即可.
解答:解:根据题意得:mx=-
,
即mx2=5,则x2=
,
则x1=
,则y1=-
=-
;
x2=-
,则y2=
,
则-9x1y2+3x2y1=-9×
•
+3×(-
)(-
)=-45+15=-30.
| 5 |
| x |
即mx2=5,则x2=
| 5 |
| m |
则x1=
|
| 5 | ||||
|
| 5m |
x2=-
|
| 5m |
则-9x1y2+3x2y1=-9×
|
| 5m |
|
| 5m |
点评:本题考查了一次函数与反比例函数的解析式,正确求得x1、x2以及对应的y1和y2的值是关键.

练习册系列答案
相关题目
在等腰三角形中,一边上的高为
,这条高与底边的夹角为60°,则此三角形面积为( )
| 3 |
| A、2 | ||||
B、2
| ||||
C、
| ||||
D、
|
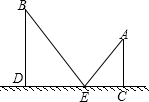 如图,在台球赛中,一球在点A处,要从A射出,经台球边挡板CD反射,击中球B.已知AC=10cm,BD=15cm,CD=xcm,EC=ycm,恰好能击中球B,求y关于x的函数解析式.
如图,在台球赛中,一球在点A处,要从A射出,经台球边挡板CD反射,击中球B.已知AC=10cm,BD=15cm,CD=xcm,EC=ycm,恰好能击中球B,求y关于x的函数解析式.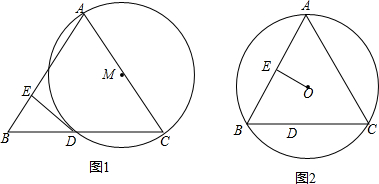
 如图,在Rt△ABC中,∠C=90°,CD⊥AB,AB=13,AC=5,以点C为圆心,
如图,在Rt△ABC中,∠C=90°,CD⊥AB,AB=13,AC=5,以点C为圆心,