题目内容
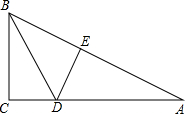 已知,如图,△ABC中,∠C=90°,AB=10,AC=8,BD为∠ABC的角平分线交AC于D,过点D作DE垂直AB于点E,
已知,如图,△ABC中,∠C=90°,AB=10,AC=8,BD为∠ABC的角平分线交AC于D,过点D作DE垂直AB于点E,(1)求AE的长;
(2)求BD的长.
考点:角平分线的性质,勾股定理
专题:
分析:(1)利用勾股定理列式求出BC,根据角平分线上的点到角的两边距离相等可得CD=DE,再利用“HL”证明Rt△BCD和Rt△BED全等,根据全等三角形对应边相等可得BE=BC,再根据AE=AB-BE计算即可得解;
(2)设CD=DE=x,利用勾股定理列式求出x,再利用勾股定理列式计算即可求出BD.
(2)设CD=DE=x,利用勾股定理列式求出x,再利用勾股定理列式计算即可求出BD.
解答:解:(1)∵∠C=90°,AB=10,AC=8,
∴BC=
=
=6,
∵BD为∠ABC的角平分线,DE⊥AB,
∴CD=DE,
在Rt△BCD和Rt△BED中,
,
∴Rt△BCD≌Rt△BED(HL),
∴BE=BC=6,
∴AE=AB-BE=10-6=4;
(2)设CD=DE=x,则AD=8-x,
在Rt△ADE中,AE2+DE2=AD2,
即42+x2=(8-x)2,
解得x=3,
所以,CD=DE=3,
在Rt△BCD中,BD=
=
=3
.
∴BC=
| AB2-AC2 |
| 102-82 |
∵BD为∠ABC的角平分线,DE⊥AB,
∴CD=DE,
在Rt△BCD和Rt△BED中,
|
∴Rt△BCD≌Rt△BED(HL),
∴BE=BC=6,
∴AE=AB-BE=10-6=4;
(2)设CD=DE=x,则AD=8-x,
在Rt△ADE中,AE2+DE2=AD2,
即42+x2=(8-x)2,
解得x=3,
所以,CD=DE=3,
在Rt△BCD中,BD=
| BC2+CD2 |
| 62+32 |
| 5 |
点评:本题考查了角平分线上的点到角的两边距离相等的性质,勾股定理,全等三角形的判定与性质,难点在于(2)多次利用勾股定理.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
在等腰三角形中,一边上的高为
,这条高与底边的夹角为60°,则此三角形面积为( )
| 3 |
| A、2 | ||||
B、2
| ||||
C、
| ||||
D、
|
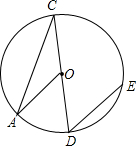 如图,CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠A的度数为( )
如图,CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠A的度数为( )| A、50° | B、40° |
| C、30° | D、25° |
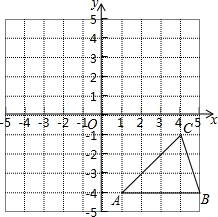 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格上,点C的坐标为(4,-1),
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格上,点C的坐标为(4,-1),
 如图,∠A=30°,∠B′=62°,△ABC与△A′B′C′关于直线l对称,则△ABC中的∠C=
如图,∠A=30°,∠B′=62°,△ABC与△A′B′C′关于直线l对称,则△ABC中的∠C=