题目内容
3. 已知,如图在矩形ABCD中,N,M分别是边AB,CD的中点,E、F分别是线段AM、BM的中点;
已知,如图在矩形ABCD中,N,M分别是边AB,CD的中点,E、F分别是线段AM、BM的中点;(1)求证:△AMD≌△BMC;
(2)判断:四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AB﹕BC=2:1时,四边形MENF是正方形(只写结论,不需证明)
分析 (1)根据矩形的性质和中点的性质、利用全等三角形的判定定理证明结论;
(2)根据三角形中位线定理和平行四边形的判定定理证明四边形MENF是平行四边形,根据全等三角形的性质得到ME=MF,根据菱形的判定定理证明;
(3)根据一个角是直角的菱形是正方形解答即可.
解答 解:(1)证明:∵四边形ABCD是矩形,
∴∠D=∠C=90°,AD=BC,
∵M是边CD的中点,
∴MD=MC,
在△AMD和△BMC中,
$\left\{\begin{array}{l}{AD=BC}\\{∠D=∠C}\\{DM=CM}\end{array}\right.$,
∴△AMD≌△BMC;
(2)四边形MENF是菱形.
证明如下:∵N、E、F分别是AB、AM、BM的中点,
∴NE∥BM,NE=$\frac{1}{2}$BM,MF=$\frac{1}{2}$BM.
∴NE=FM,NE∥FM.
∴四边形MENF是平行四边形,
∵△AMD≌△BMC,
∴AM=BM,
∵E、F分别是AM、BM的中点,
∴ME=MF.
∴平行四边形MENF是菱形;
(3)2:1,
当AB﹕BC=2:1时,DA=DM,
∴∠DAM=∠DMA=45°,
同理∠CMB=∠CBM=45°,
∴∠AMB=90°,
∴四边形MENF是正方形.
故答案为:2:1.
点评 本题考查的是矩形的性质、菱形的判定、正方形的判定和三角形中位线定理的应用以及全等三角形的判定和性质,掌握相关的性质定理、灵活运用三角形中位线定理是解题的关键,

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
13.据报道,投资270亿元的西环高铁预计今年底建成通车,通车后能使西环高铁经过的市县约4360000人受益,数据4360000用科学记数法表示为( )
| A. | 436×104 | B. | 4.36×105 | C. | 4.36×106 | D. | 4.36×107 |
11.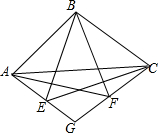 如图,Rt△ABC中,∠ABC=90°,以BA、BC为边向内作等边ABF和等边BCE,AE与CF交于G点,以下结论:①AE=CF;②∠AGC=120°;③GB平分∠AGC;④若AB=BC,则AE=2EG,其中正确的结论有( )
如图,Rt△ABC中,∠ABC=90°,以BA、BC为边向内作等边ABF和等边BCE,AE与CF交于G点,以下结论:①AE=CF;②∠AGC=120°;③GB平分∠AGC;④若AB=BC,则AE=2EG,其中正确的结论有( )
 如图,Rt△ABC中,∠ABC=90°,以BA、BC为边向内作等边ABF和等边BCE,AE与CF交于G点,以下结论:①AE=CF;②∠AGC=120°;③GB平分∠AGC;④若AB=BC,则AE=2EG,其中正确的结论有( )
如图,Rt△ABC中,∠ABC=90°,以BA、BC为边向内作等边ABF和等边BCE,AE与CF交于G点,以下结论:①AE=CF;②∠AGC=120°;③GB平分∠AGC;④若AB=BC,则AE=2EG,其中正确的结论有( )| A. | ①②③ | B. | ①②③④ | C. | ①②④ | D. | ②③④ |
18.分式$\frac{1}{|x|-1}$无意义,则x的值为( )
| A. | ±1 | B. | -1 | C. | 1 | D. | 0 |
13.2016年2月上旬福州地区空气质量指数(AQI)如下表所示,空气质量指数不大于100表示空气质量优良,
2016年2月上旬福州地区空气质量指数(AQI)
如果小王该月上旬来福州度假三天那么他在福州度假期间空气质量都是优良的概率是$\frac{5}{8}$.
2016年2月上旬福州地区空气质量指数(AQI)
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ug/m3 | 26 | 34 | 43 | 41 | 34 | 48 | 78 | 1 15 | 59 | 45 |
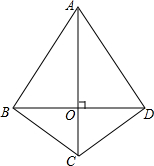 如图,AC、BD相交于点O,且AB=AD.求证:
如图,AC、BD相交于点O,且AB=AD.求证: