题目内容
14.已知一个直角三角形的两条边长分别为3cm和4cm,则这个直角三角形的内切圆的半径为1cm.分析 先用勾股定理求出斜边,再利用直角三角形的内切圆半径等于两直角边的和与斜边之差的一半,计算出内切圆的半径.
解答 解:斜边=$\sqrt{{3}^{2}+{4}^{2}}=5$cm,则此直角三角形的内切圆半径=$\frac{3+4-5}{2}$=1cm.
故答案为:1
点评 此题考查三角形的内切圆问题,熟悉勾股定理,记住直角三角形的内切圆半径等于两直角边的和与斜边之差的一半这个结论是解题的关键.

练习册系列答案
相关题目
4.下列计算中,正确的是( )
| A. | (a2)3=a5 | B. | a3÷a2=1 | C. | a2+a2=a4 | D. | 4a-3a=a |

 如图,矩形ABCD的边长是常量,点E在AD上以每秒3个单位的速度从D运动到A,当运动时间为1秒时,△ABE的面积为10;当运动时间为2秒时,△ABE的面积为4.
如图,矩形ABCD的边长是常量,点E在AD上以每秒3个单位的速度从D运动到A,当运动时间为1秒时,△ABE的面积为10;当运动时间为2秒时,△ABE的面积为4.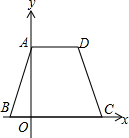 边BC在x轴上,点A在y轴的正方向上,A(0,6),D (4,6),且AB=2$\sqrt{10}$
边BC在x轴上,点A在y轴的正方向上,A(0,6),D (4,6),且AB=2$\sqrt{10}$ 已知,如图在矩形ABCD中,N,M分别是边AB,CD的中点,E、F分别是线段AM、BM的中点;
已知,如图在矩形ABCD中,N,M分别是边AB,CD的中点,E、F分别是线段AM、BM的中点;