题目内容
12.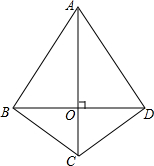 如图,AC、BD相交于点O,且AB=AD.求证:
如图,AC、BD相交于点O,且AB=AD.求证:(1)BO=DO;
(2)BC=DC.
分析 (1)证明Rt△AOB≌Rt△AOD,根据全等三角形的对应边相等,即可解答;
(2)证明△BOC≌△DOC,根据全等三角形的对应边相等,即可解答.
解答 解:(1)∵AC⊥BD,
∴∠AOB=∠AOD=90°,
在Rt△AOB和Rt△AOD,
$\left\{\begin{array}{l}{AB=AD}\\{AO=AO}\end{array}\right.$
∴Rt△AOB≌Rt△AOD,
∴BO=DO.
(2)在△BOC和△DOC中,
$\left\{\begin{array}{l}{BO=DO}\\{∠BOC=∠DOC=90°}\\{OC=OC}\end{array}\right.$
∴△BOC≌△DOC,
∴BC=DC.
点评 本题考查了全等三角形的性质定理和判定定理,解决本题的关键是证明三角形全等.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
20.3tan30°的值等于( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
4.下列计算中,正确的是( )
| A. | (a2)3=a5 | B. | a3÷a2=1 | C. | a2+a2=a4 | D. | 4a-3a=a |
2.下列说法中,正确的是( )
| A. | 关于某条直线对称的两个三角形一定全等 | |
| B. | 两个全等三角形一定关于某条直线对称 | |
| C. | 面积相等的两个三角形一定关于某条直线之间对称 | |
| D. | 周长相等的两个三角形一定关于某条直线之间对称 |
 已知,如图在矩形ABCD中,N,M分别是边AB,CD的中点,E、F分别是线段AM、BM的中点;
已知,如图在矩形ABCD中,N,M分别是边AB,CD的中点,E、F分别是线段AM、BM的中点;