题目内容
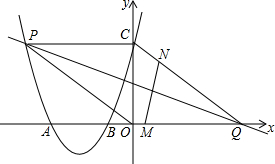 如图,二次函数的图象与x轴相交于点A(-3,0)、B(-1,0),与y轴相交于点C(0,3),点P是该图象上的动点,点Q的坐标为(4,0).
如图,二次函数的图象与x轴相交于点A(-3,0)、B(-1,0),与y轴相交于点C(0,3),点P是该图象上的动点,点Q的坐标为(4,0).(1)求该二次函数的表达式;
(2)当OP∥CQ时,求点P的坐标;
(3)点M,N分别在线段AQ、CQ上,点M以每秒3个单位长度的速度从点A向点Q运动,同时,点N以每秒1个单位长度的速度从点C向点Q运动,当点M,N中有一点到达Q点时,两点同时停止运动.设运动时间为t秒,当直线PQ垂直平分线段MN时,请求出此时t的值及点P的坐标.
考点:二次函数综合题
专题:
分析:(1)设抛物线的解析式为:y=ax2+bx+c,把A,B,C三点的坐标代入求出a,b,c的值即可;
(2)过P作PH⊥AB于H,首先利用已知条件求出PH和OH的比值为3:4,再设PH=3m,则OH=4m,代入抛物线的解析式求出m的值即可求出P的坐标;
(3)当线PQ垂直平分线段MN时,直线PQ上的点到∠AQC两边的距离相等,则直线PQ能平分∠AQC,由此可求出t的值及点P的坐标.
(2)过P作PH⊥AB于H,首先利用已知条件求出PH和OH的比值为3:4,再设PH=3m,则OH=4m,代入抛物线的解析式求出m的值即可求出P的坐标;
(3)当线PQ垂直平分线段MN时,直线PQ上的点到∠AQC两边的距离相等,则直线PQ能平分∠AQC,由此可求出t的值及点P的坐标.
解答:解:(1)设抛物线的解析式为:y=ax2+bx+c,
∵抛物线经过点C(0,3),
∴c=3.
把A(-3,0)、B(-1,0)代入y=ax2+bx+3中得
,
解得
.
∴抛物线的解析式为:y=x2+4x+3;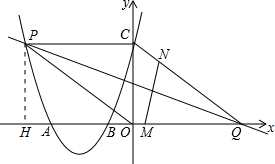
(2)过P作PH⊥AB于H,
∵OP∥CQ,
∴∠POH=∠CQO,
∴tan∠POH=tan∠CQO=
=
,
∴
=
,
设PH=3m,则OH=4m,
∴点P的坐标为(-4m,3m)
将其代入y=x2+4x+3得:16m-16m+3=3m,
解得:m=1,
∴P的坐标为(-4,3);
(3)过点N作ND⊥x轴于点D,则ND∥OC,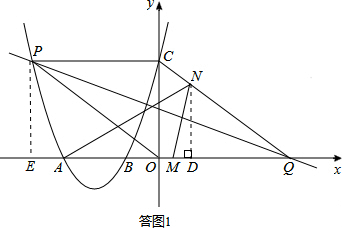 (如图1)
(如图1)
因为直线PQ能够垂直平分线段MN,则有QM=QN,且PQ⊥MN,PQ平分∠AQC.
由QM=QN,得:7-3t=5-t,解得t=1.
设P(x,x2+4x+3),
若直线PQ⊥MN,则:过P作直线PE⊥x轴,垂足为E,
则△PEQ∽△MDN,
∴
=
,
∴
=
,
∴x=
,
∴P(
,
)或(
,
).
∵抛物线经过点C(0,3),
∴c=3.
把A(-3,0)、B(-1,0)代入y=ax2+bx+3中得
|
解得
|
∴抛物线的解析式为:y=x2+4x+3;

(2)过P作PH⊥AB于H,
∵OP∥CQ,
∴∠POH=∠CQO,
∴tan∠POH=tan∠CQO=
| OC |
| OQ |
| 3 |
| 4 |
∴
| PH |
| OH |
| 3 |
| 4 |
设PH=3m,则OH=4m,
∴点P的坐标为(-4m,3m)
将其代入y=x2+4x+3得:16m-16m+3=3m,
解得:m=1,
∴P的坐标为(-4,3);
(3)过点N作ND⊥x轴于点D,则ND∥OC,
 (如图1)
(如图1)因为直线PQ能够垂直平分线段MN,则有QM=QN,且PQ⊥MN,PQ平分∠AQC.
由QM=QN,得:7-3t=5-t,解得t=1.
设P(x,x2+4x+3),
若直线PQ⊥MN,则:过P作直线PE⊥x轴,垂足为E,
则△PEQ∽△MDN,
∴
| PE |
| EQ |
| MD |
| ND |
∴
| x2+4x+3 |
| 4-x |
| ||
|
∴x=
-13±
| ||
| 6 |
∴P(
-13-
| ||
| 6 |
37+
| ||
| 18 |
-13+
| ||
| 6 |
37-
| ||
| 18 |
点评:本题是二次函数综合题型,考查了二次函数的图象与性质、待定系数法、一次函数、相似三角形、平行四边形、角平分线的性质、二次函数的最值等知识点.试题难度不大.

练习册系列答案
相关题目
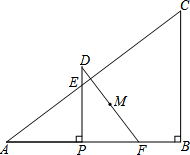 如图,在Rt△ABC中,∠B=90°,AB=20cm,BC=15cm,动点P从点A出发,以每秒4cm的速度沿AB方向运动,到达点B时停止运动.过点P作AB的垂线交斜边AC于点E,将△APE绕点P顺时针旋转90°得到△DPF.设点P在边AB上运动的时间为t(秒).
如图,在Rt△ABC中,∠B=90°,AB=20cm,BC=15cm,动点P从点A出发,以每秒4cm的速度沿AB方向运动,到达点B时停止运动.过点P作AB的垂线交斜边AC于点E,将△APE绕点P顺时针旋转90°得到△DPF.设点P在边AB上运动的时间为t(秒).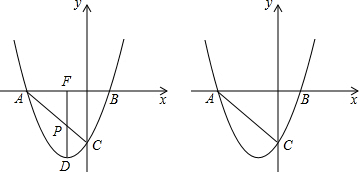
 如图所示,某河堤的横断面是梯形ABCD,BC∥AD,迎水坡AB长26米,且斜坡AB的坡度为
如图所示,某河堤的横断面是梯形ABCD,BC∥AD,迎水坡AB长26米,且斜坡AB的坡度为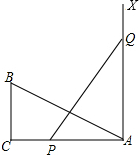 如图,BC、AX分别垂直于AC,AC=2BC,点P和点Q从A点出发分别在AC和射线AX上运动,且点Q的运动速度是点P运动速度的2倍,当点P运动到
如图,BC、AX分别垂直于AC,AC=2BC,点P和点Q从A点出发分别在AC和射线AX上运动,且点Q的运动速度是点P运动速度的2倍,当点P运动到