题目内容
抛物线y=ax2+bx-3经过点A、B、C,其中A(-3,0),B(1,0).
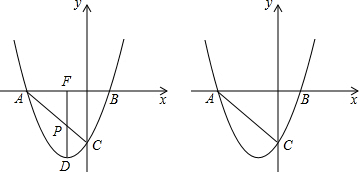
(1)求此抛物线的解析式;
(2)如图,P为线段AC上一点,过点P作y轴的平行线交抛物线于点D,交x轴于点F:
①当△ADC的面积最大时,求点P的坐标;
②设M(m,0)是x轴上一动点,点N是线段DF上一点,当△ADC的面积最大时,若∠MNC=90°,请求出实数m的取值范围.

(1)求此抛物线的解析式;
(2)如图,P为线段AC上一点,过点P作y轴的平行线交抛物线于点D,交x轴于点F:
①当△ADC的面积最大时,求点P的坐标;
②设M(m,0)是x轴上一动点,点N是线段DF上一点,当△ADC的面积最大时,若∠MNC=90°,请求出实数m的取值范围.
考点:二次函数综合题
专题:
分析:(1)由y=ax2+bx-3经过点A(-3,0),B(1,0)利用待定系数法即可求得此抛物线的解析式;
(2)首先令x=0,求得点C的坐标,然后设直线BC的解析式为y=kx+b′,由待定系数法求得直线BC的解析式为y=-x+3,再设P(a,3-a),即可得D(a,-a2+2a+3),求出PD的长,由S△BDC=S△PDC+S△PDB,得到S△BDC=-
(a-
)2+
,利用二次函数的性质,即可求得当△BDC的面积最大时,点P的坐标;
(3)将x=
代入抛物线解析式y=-x2+2x+3求出点P的纵坐标,过点C作CG⊥DF,然后分①点N在DG上时,点N与点D重合时,点M的横坐标最大,然后根据勾股定理得出CD2+DM2=CM2,列出关于m的方程,解方程求出m的最大值;②点N在线段GF上时,设GN=x,然后表示出NF,根据同角的余角相等求出∠NCG=∠MNF,然后证明△NCG和△MNF相似,根据相似三角形对应边成比例列出比例式用x表示出MF,再根据二次函数的最值问题求出y的最大值,然后求出MO,从而得到点M的坐标,求出m的最小值.
(2)首先令x=0,求得点C的坐标,然后设直线BC的解析式为y=kx+b′,由待定系数法求得直线BC的解析式为y=-x+3,再设P(a,3-a),即可得D(a,-a2+2a+3),求出PD的长,由S△BDC=S△PDC+S△PDB,得到S△BDC=-
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
(3)将x=
| 3 |
| 2 |
解答:解:(1)由题意得:
,
解得:
.
故抛物线解析式为y=x2+2x-3;
(2)令x=0,则y=-3,即C(0,-3).
设直线AC的解析式为y=kx+b′,
则
,解得:
,
故直线AC的解析式为y=-x-3.
设P(a,-a-3),则D(a,a2+2a-3),
∴PD=(-a-3)-(a2+2a-3)=-a2-3a,
∴S△ADC=S△PDC+S△PDA=
PD•(-a)+
PD•(a+3)=
PD•3=
(-a2-3a)=-
(a+
)2+
,
∴当a=-
时,△BDC的面积最大,此时P(-
,-
);
(3)将x=-
代入y=x2+2x-3,得y=(-
)2+2×(-
)-3=-
,
∴点D的坐标为(-
,-
).
如图,过点C作CG⊥DF,则CG=
.
①点N在DG上时,点N与点D重合时,点M的横坐标最小.
∵∠MNC=90°,∴CD2+DM2=CM2,
∵C(0,-3),D(-
,-
),M(m,0),
∴(0+
)2+(-
+3)2+(m+
)2+(0+
)2=(m-0)2+(0+3)2,
解得m=-
.
∴点M的坐标为( 0,0),
即m的最小值为-
;
②点N在线段GF上时,设GN=x,则NF=3-x,
∵∠MNC=90°,
∴∠CNG+∠MNF=90°,
又∵∠CNG+∠NCG=90°,
∴∠NCG=∠MNF,
又∵∠NGC=∠MFN=90°,
∴Rt△NCG∽△MNF,
∴
=
,即
=
,
整理得,MF=-
x2+2x=-
(x-
)2+
,
∴当x=
时(N与P重合),MF有最大值
,
此时M与O重合,
∴M的坐标为(0,0),
∴m的最大值为0,
故实数m的变化范围为-
≤m≤0.
|
解得:
|
故抛物线解析式为y=x2+2x-3;
(2)令x=0,则y=-3,即C(0,-3).
设直线AC的解析式为y=kx+b′,
则
|
|
故直线AC的解析式为y=-x-3.
设P(a,-a-3),则D(a,a2+2a-3),
∴PD=(-a-3)-(a2+2a-3)=-a2-3a,
∴S△ADC=S△PDC+S△PDA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
∴当a=-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
(3)将x=-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 15 |
| 4 |
∴点D的坐标为(-
| 3 |
| 2 |
| 15 |
| 4 |
如图,过点C作CG⊥DF,则CG=
| 3 |
| 2 |

①点N在DG上时,点N与点D重合时,点M的横坐标最小.
∵∠MNC=90°,∴CD2+DM2=CM2,
∵C(0,-3),D(-
| 3 |
| 2 |
| 15 |
| 4 |
∴(0+
| 3 |
| 2 |
| 15 |
| 4 |
| 3 |
| 2 |
| 15 |
| 4 |
解得m=-
| 27 |
| 8 |
∴点M的坐标为( 0,0),
即m的最小值为-
| 27 |
| 8 |
②点N在线段GF上时,设GN=x,则NF=3-x,
∵∠MNC=90°,
∴∠CNG+∠MNF=90°,
又∵∠CNG+∠NCG=90°,
∴∠NCG=∠MNF,
又∵∠NGC=∠MFN=90°,
∴Rt△NCG∽△MNF,
∴
| CG |
| NF |
| GN |
| MF |
| ||
| 3-x |
| x |
| MF |
整理得,MF=-
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
∴当x=
| 3 |
| 2 |
| 3 |
| 2 |
此时M与O重合,
∴M的坐标为(0,0),
∴m的最大值为0,
故实数m的变化范围为-
| 27 |
| 8 |
点评:此题考查了待定系数法求函数的解析式、三角形的面积、相似三角形的判定与性质、二次函数的最值、勾股定理等知识.此题综合性很强,难度较大,注意掌握数形结合思想、分类讨论思想与方程思想的应用.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目

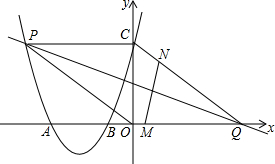 如图,二次函数的图象与x轴相交于点A(-3,0)、B(-1,0),与y轴相交于点C(0,3),点P是该图象上的动点,点Q的坐标为(4,0).
如图,二次函数的图象与x轴相交于点A(-3,0)、B(-1,0),与y轴相交于点C(0,3),点P是该图象上的动点,点Q的坐标为(4,0).