题目内容
如图所示，某河堤的横断面是梯形ABCD，BC∥AD，迎水坡AB长26米，且斜坡AB的坡度为| 12 |
| 5 |
考点：解直角三角形的应用-坡度坡角问题
专题：
分析：由已知斜坡AB的坡度
，可得到BE、AE的比例关系，进而由勾股定理求得BE、AE的长，由此得解．
| 12 |
| 5 |
解答：解：由已知斜坡AB的坡度
，得：
BE：AE=12：5，
设AE=5x，则BE=12x，
在直角三角形AEB中，根据勾股定理得：
262=5x2+（12x）2，
即169x2=676，
解得：x=2或x=-2（舍去），
5x=10，12x=24
即河堤高BE等于24米．
故答案为：24．
| 12 |
| 5 |
BE：AE=12：5，
设AE=5x，则BE=12x，
在直角三角形AEB中，根据勾股定理得：
262=5x2+（12x）2，
即169x2=676，
解得：x=2或x=-2（舍去），
5x=10，12x=24
即河堤高BE等于24米．
故答案为：24．
点评：本题主要考查的是坡度的定义和勾股定理的应用，解题的关键是从图中抽象出直角三角形，难度不大．
练习册系列答案
相关题目
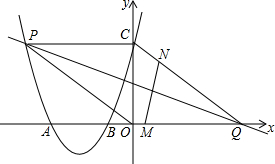如图，二次函数的图象与x轴相交于点A（-3，0）、B（-1，0），与y轴相交于点C（0，3），点P是该图象上的动点，点Q的坐标为（4，0）．
如图，在△ABC中，∠C=90°，作AB的垂直平分线，交AB于点D，交AC于点E，连接BE，若DE=CE．