题目内容
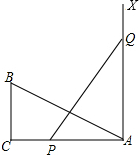 如图,BC、AX分别垂直于AC,AC=2BC,点P和点Q从A点出发分别在AC和射线AX上运动,且点Q的运动速度是点P运动速度的2倍,当点P运动到
如图,BC、AX分别垂直于AC,AC=2BC,点P和点Q从A点出发分别在AC和射线AX上运动,且点Q的运动速度是点P运动速度的2倍,当点P运动到考点:全等三角形的判定
专题:动点型
分析:根据垂直得出∠C=∠PAQ=90°,根据已知得出AP=BC,AQ=AC时两三角形全等,即可得出答案.
解答:解:∵BC、AX分别垂直于AC,
∴∠C=∠PAQ=90°,
∵点Q的运动速度是点P运动速度的2倍,
∴设AP=t,则AQ=2t,
即AQ=2AP,
∵AC=2BC,
∴要使△ABC与△APQ全等,一定是AP=BC,AQ=AC,
∵AX=2BC,
∴当P运动到AC的中点时,△ABC与△APQ一定全等,
故答案为:AC的中点.
∴∠C=∠PAQ=90°,
∵点Q的运动速度是点P运动速度的2倍,
∴设AP=t,则AQ=2t,
即AQ=2AP,
∵AC=2BC,
∴要使△ABC与△APQ全等,一定是AP=BC,AQ=AC,
∵AX=2BC,
∴当P运动到AC的中点时,△ABC与△APQ一定全等,
故答案为:AC的中点.
点评:本题考查了全等三角形的判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2008年5月12日四川汶川发生里氏8.0级大地震,国内外社会各界纷纷向灾区捐款捐物,抗震救灾,截至6月4日12时,全国共接收捐款约为43700000000元人民币.这笔款额用科学记数法表示正确的是( )
| A、0.437×1011 |
| B、4.4×1010 |
| C、4.37×1010 |
| D、43.7×109 |
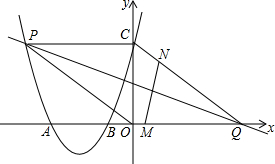 如图,二次函数的图象与x轴相交于点A(-3,0)、B(-1,0),与y轴相交于点C(0,3),点P是该图象上的动点,点Q的坐标为(4,0).
如图,二次函数的图象与x轴相交于点A(-3,0)、B(-1,0),与y轴相交于点C(0,3),点P是该图象上的动点,点Q的坐标为(4,0).