题目内容
18.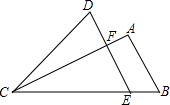 如图,E为△ABC的BC边上一点,DE∥AB交AC于F,连接CD,若S△ABC=S△DCE,且EF=9,AB=12,则DF的长为7.
如图,E为△ABC的BC边上一点,DE∥AB交AC于F,连接CD,若S△ABC=S△DCE,且EF=9,AB=12,则DF的长为7.
分析 已知△CDF与四边形AFEB的面积相等,再根据相似三角形的相似比求得它们的面积关系比,从而求DF的长.
解答 解:∵△ABC与△DEC的面积相等,
∴△CDF与四边形AFEB的面积相等,
∵AB∥DE,
∴△CEF∽△CBA,
∵EF=9,AB=12,
∴$\frac{EF}{AB}=\frac{9}{12}=\frac{3}{4}$,
∴$\frac{{S}_{△CEF}}{{S}_{△CBA}}=\frac{9}{16}$,
设△CEF的面积为9k,则四边形AFEB的面积=7k,
∵△CDF与四边形AFEB的面积相等,
∴△CDF=7k,
∵△CDF与△CEF是同高不同底的三角形,
∴它们的面积比等于底之比,
∴$\frac{DF}{EF}=\frac{7k}{9k}$,
∴DF=7.
故答案为:7.
点评 本题考查了相似三角形的判定和性质,图形的面积,知道同高不同底的三角形它们的面积比等于底之比是解题的关键.

练习册系列答案
相关题目
13. 美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感,如图,某女士身高165cm,下半身长x与身高L的比值为0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )
美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感,如图,某女士身高165cm,下半身长x与身高L的比值为0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )
 美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感,如图,某女士身高165cm,下半身长x与身高L的比值为0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )
美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感,如图,某女士身高165cm,下半身长x与身高L的比值为0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )| A. | 10cm | B. | 7.8cm | C. | 6.5cm | D. | 5cm |
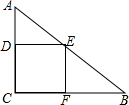 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点E在AB上,点D在AC上,若矩形DEFC的面积为12,则这个矩形的长和宽分别是多少?
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点E在AB上,点D在AC上,若矩形DEFC的面积为12,则这个矩形的长和宽分别是多少?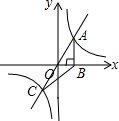 如图,已知反比例函数y=$\frac{k}{x}$(k≠0)与直线y=x交于A、C两点,AB⊥x轴于点B,若S△ABC=6,则反比例函数的解析式为y=$\frac{6}{x}$.
如图,已知反比例函数y=$\frac{k}{x}$(k≠0)与直线y=x交于A、C两点,AB⊥x轴于点B,若S△ABC=6,则反比例函数的解析式为y=$\frac{6}{x}$.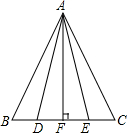 在△ABC中,AB=AC,AF⊥BC,BD=CE,则图中全等三角形共有4对.
在△ABC中,AB=AC,AF⊥BC,BD=CE,则图中全等三角形共有4对.