题目内容
8.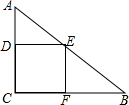 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点E在AB上,点D在AC上,若矩形DEFC的面积为12,则这个矩形的长和宽分别是多少?
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点E在AB上,点D在AC上,若矩形DEFC的面积为12,则这个矩形的长和宽分别是多少?
分析 设DC=x,则AD=6-x,根据矩形的性质得到DE∥BC,EF∥AC,推出△ADE∽△ACB,根据相似三角形的性质得到$\frac{AD}{AC}=\frac{DE}{BC}$,代入数据得到DE=8-$\frac{4}{3}x$,根据矩形的面积列方程x(8-$\frac{4}{3}x$)=12,即可得到结论.
解答 解:设DC=x,则AD=6-x,
∵矩形DEFC,
∴DE∥BC,EF∥AC,
∴△ADE∽△ACB,
∴$\frac{AD}{AC}=\frac{DE}{BC}$,
即$\frac{6-x}{6}=\frac{DE}{8}$,
∴DE=8-$\frac{4}{3}x$,
∵矩形DEFC的面积为12,
∴x(8-$\frac{4}{3}x$)=12,
解得:x=3,DE=8-$\frac{4}{3}×3$=4,
∴这个矩形的长和宽分别是4,3.
点评 本题考查了相似三角形的判定和性质,矩形的性质,矩形的面积公式,熟练掌握相似三角形的性质定理是解题的关键.

练习册系列答案
相关题目
20.某生活小区鲜奶店每天以每瓶3元的价格从奶场购进优质鲜奶,然后以每瓶5元的价格出售,如果当天卖不完,剩余的只有倒掉.店主记录了30天的日需求量(单位:瓶),整理得下表:
(1)求这30天内日需求量的众数和中位数;
(2)如果一年按365天计算,试估计一年中鲜奶店的总利润(单位:元).
| 日需求量 | 26 | 27 | 28 | 29 | 31 |
| 天数 | 5 | 8 | 7 | 6 | 4 |
(2)如果一年按365天计算,试估计一年中鲜奶店的总利润(单位:元).
13.已知∠A,∠B均为锐角,且cosA=$\frac{1}{2}$,sinB=$\frac{1}{2}$,则下列结论中正确的是( )
| A. | ∠A=∠B=60° | B. | ∠A=∠B=30° | C. | ∠A=30°,∠B=60° | D. | ∠A=60°,∠B=30° |
 如图,已知⊙O是△ABC的内切圆,切点为D、E、F,如果AE=1,CD=2,BF=3,且△ABC的面积为6,求内切圆的半径r.
如图,已知⊙O是△ABC的内切圆,切点为D、E、F,如果AE=1,CD=2,BF=3,且△ABC的面积为6,求内切圆的半径r.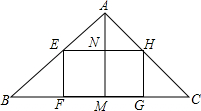 在△ABC中,己知BC=20cm,BC边上的高AM=16cm,在三角形内截取一个面积最大的矩形,并使它的一边在BC上,求此时矩形的长和宽.
在△ABC中,己知BC=20cm,BC边上的高AM=16cm,在三角形内截取一个面积最大的矩形,并使它的一边在BC上,求此时矩形的长和宽.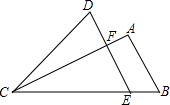 如图,E为△ABC的BC边上一点,DE∥AB交AC于F,连接CD,若S△ABC=S△DCE,且EF=9,AB=12,则DF的长为7.
如图,E为△ABC的BC边上一点,DE∥AB交AC于F,连接CD,若S△ABC=S△DCE,且EF=9,AB=12,则DF的长为7.