题目内容
6.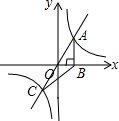 如图,已知反比例函数y=$\frac{k}{x}$(k≠0)与直线y=x交于A、C两点,AB⊥x轴于点B,若S△ABC=6,则反比例函数的解析式为y=$\frac{6}{x}$.
如图,已知反比例函数y=$\frac{k}{x}$(k≠0)与直线y=x交于A、C两点,AB⊥x轴于点B,若S△ABC=6,则反比例函数的解析式为y=$\frac{6}{x}$.
分析 过C作CD⊥x轴于D,设A的坐标是(a,b),根据双曲线的性质得到C的坐标是(-a,-b),根据三角形的面积公式推出$\frac{1}{2}$ab+$\frac{1}{2}$ab=6,代入即可求出k.
解答  解:过C作CD⊥x轴于D,
解:过C作CD⊥x轴于D,
设A的坐标是(a,b),则根据双曲线的两个分支关于原点对称,则C的坐标是(-a,-b),
则ab=k,OB=a,AB=b,CD=b,
∵S△ABC=S△AOB+S△COB=4,
∴$\frac{1}{2}$ab+$\frac{1}{2}$ab=6,
即$\frac{1}{2}$k+$\frac{1}{2}$k=6,
解得k=6,
故该反比例函数解析式为:y=$\frac{6}{x}$.
故答案为:y=$\frac{6}{x}$.
点评 本题主要考查对三角形的面积,反比例函数的性质,一次函数与反比例函数的交点问题等知识点的理解和掌握,能推出$\frac{1}{2}$k+$\frac{1}{2}$k=6是解此题的关键.

练习册系列答案
相关题目
20.某生活小区鲜奶店每天以每瓶3元的价格从奶场购进优质鲜奶,然后以每瓶5元的价格出售,如果当天卖不完,剩余的只有倒掉.店主记录了30天的日需求量(单位:瓶),整理得下表:
(1)求这30天内日需求量的众数和中位数;
(2)如果一年按365天计算,试估计一年中鲜奶店的总利润(单位:元).
| 日需求量 | 26 | 27 | 28 | 29 | 31 |
| 天数 | 5 | 8 | 7 | 6 | 4 |
(2)如果一年按365天计算,试估计一年中鲜奶店的总利润(单位:元).
11.若两个连续整数的积为56,则这两个连续整数的和为( )
| A. | 15 | B. | -15 | C. | ±15 | D. | -1 |
15.抛物线y=(x+2)2-1的顶点坐标是( )
| A. | (2,1) | B. | (-2,-1) | C. | (-2,1) | D. | (2,-1) |

 如图,△ABC在平面直角坐标系中第二象限内,顶点A的坐标是(-2,3),先把△ABC向右平移4个单位得到△A1B1C1,再作△A1B1C1关于x轴对称图形△A2B2C2,则顶点A2的坐标是(2,-3).
如图,△ABC在平面直角坐标系中第二象限内,顶点A的坐标是(-2,3),先把△ABC向右平移4个单位得到△A1B1C1,再作△A1B1C1关于x轴对称图形△A2B2C2,则顶点A2的坐标是(2,-3).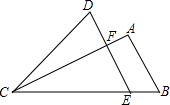 如图,E为△ABC的BC边上一点,DE∥AB交AC于F,连接CD,若S△ABC=S△DCE,且EF=9,AB=12,则DF的长为7.
如图,E为△ABC的BC边上一点,DE∥AB交AC于F,连接CD,若S△ABC=S△DCE,且EF=9,AB=12,则DF的长为7.