题目内容
8.点(-2,3)在正比例函数y=kx的直线上,则k=-$\frac{3}{2}$.分析 直接把点(-2,3)代入正比例函数y=kx,求出k的值即可.
解答 解:∵点(-2,3)在正比例函数y=kx的直线上,
∴3=-2k,解得k=-$\frac{3}{2}$.
故答案为:-$\frac{3}{2}$.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
3.某市商品房的均价原为18150元/m2,经过连续两次降价后均价为15000元/m2.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
| A. | 18150(1-x)2=18150-15000 | B. | 18150(1-x2)=15000 | ||
| C. | 18150(1-2x)=15000 | D. | 18150(1-x)2=15000 |
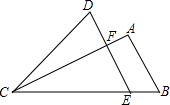 如图,E为△ABC的BC边上一点,DE∥AB交AC于F,连接CD,若S△ABC=S△DCE,且EF=9,AB=12,则DF的长为7.
如图,E为△ABC的BC边上一点,DE∥AB交AC于F,连接CD,若S△ABC=S△DCE,且EF=9,AB=12,则DF的长为7. 已知,如图,△ABC中,∠A=90°,AB=AC,D是BC边上的中点,E、F分别是AB、AC上的点,且∠EDF=90°,求证:BE=AF.
已知,如图,△ABC中,∠A=90°,AB=AC,D是BC边上的中点,E、F分别是AB、AC上的点,且∠EDF=90°,求证:BE=AF. 如图,排球运动员站在距球网B的水平距离4m的点O处发球,将球从O点正上方2.25m的A处发出,把球看成点,其运行的水平距离x为2.5m达到的最大高度y为3.5m,球场的边界距O点的水平距离为10m.
如图,排球运动员站在距球网B的水平距离4m的点O处发球,将球从O点正上方2.25m的A处发出,把球看成点,其运行的水平距离x为2.5m达到的最大高度y为3.5m,球场的边界距O点的水平距离为10m.