题目内容
 八年级(5)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.小明同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20cm,宽AB=16cm的长方形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的点F处,…请你根据①②步骤解答下列问题:
八年级(5)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.小明同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20cm,宽AB=16cm的长方形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的点F处,…请你根据①②步骤解答下列问题:(1)找出图中由折叠可知的相等线段.
(2)计算EC的长.
考点:翻折变换(折叠问题)
专题:
分析:(1)如图,由折叠变换的性质找出相等的线段,即可解决问题.
(2)首先求出BF的长,进而求出CF的长;运用勾股定理列出关于EF的方程,求出EF即可解决问题.
(2)首先求出BF的长,进而求出CF的长;运用勾股定理列出关于EF的方程,求出EF即可解决问题.
解答: 解:(1)如图,由折叠变换的性质知:
解:(1)如图,由折叠变换的性质知:
AD=AF,DE=EF.
(2)∵四边形ABCD为矩形,
∴AD=BC=20,CD=AB=16;∠B=∠C=90°
∴AF=AD=20;由勾股定理得:
BF=
=12,
∴CF=20-12=8;设DE=EF=λ,
∴EC=16-λ;由勾股定理得:
λ2=(16-λ)2+82,解得:λ=10,
∴EC=16-10=6(cm).
 解:(1)如图,由折叠变换的性质知:
解:(1)如图,由折叠变换的性质知:AD=AF,DE=EF.
(2)∵四边形ABCD为矩形,
∴AD=BC=20,CD=AB=16;∠B=∠C=90°
∴AF=AD=20;由勾股定理得:
BF=
| AF2-AB2 |
∴CF=20-12=8;设DE=EF=λ,
∴EC=16-λ;由勾股定理得:
λ2=(16-λ)2+82,解得:λ=10,
∴EC=16-10=6(cm).
点评:该题主要考查了翻折变换的性质、矩形的性质、勾股定理等知识点的应用问题;对综合的分析问题解决问题的能力提出了一定的要求.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
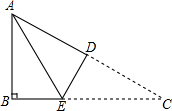 如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则BE的长为( )
如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则BE的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
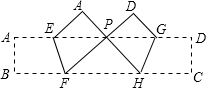 把长方形纸条ABCD沿EF,GH同时折叠,B、C两点恰好都落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则长方形ABCD的面积为多少?
把长方形纸条ABCD沿EF,GH同时折叠,B、C两点恰好都落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则长方形ABCD的面积为多少?