题目内容
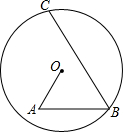 如图,在圆O中,点A在圆内,B,C在圆上,其中OA=7,BC=18,∠A=∠B=60°,则OB=
如图,在圆O中,点A在圆内,B,C在圆上,其中OA=7,BC=18,∠A=∠B=60°,则OB=考点:垂径定理,等边三角形的判定与性质,勾股定理
专题:
分析:过O作OD⊥BC,延长AO,交BC于点E,连接OB,由∠A=∠B=60°,得到三角形ABE为等边三角形,确定出∠AEB与∠EOD的度数,在直角三角形ODE中,设DE=x,表示出OE与OD,根据AE=BE列出关于x的方程,求出方程的解得到x的值,确定出OD的长,
解答: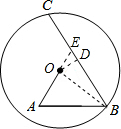 解:过O作OD⊥BC,延长AO,交BC于点E,连接OB,
解:过O作OD⊥BC,延长AO,交BC于点E,连接OB,
∵∠A=∠B=60°,
∴∠OED=60°,∠EOD=30°,
在Rt△ODE中,设DE=x,则OE=2x,OD=
x,
∵OD⊥BC,
∴D为BC的中点,
即BD=CD=
BC=9,
∵AE=BE,
∴7+2x=9+x,
解得:x=2,即OD=2
,
∴OB=
=
=
.
故答案为:
.
 解:过O作OD⊥BC,延长AO,交BC于点E,连接OB,
解:过O作OD⊥BC,延长AO,交BC于点E,连接OB,∵∠A=∠B=60°,
∴∠OED=60°,∠EOD=30°,
在Rt△ODE中,设DE=x,则OE=2x,OD=
| 3 |
∵OD⊥BC,
∴D为BC的中点,
即BD=CD=
| 1 |
| 2 |
∵AE=BE,
∴7+2x=9+x,
解得:x=2,即OD=2
| 3 |
∴OB=
| OD2+BD2 |
(2
|
| 93 |
故答案为:
| 93 |
点评:此题考查了垂径定理,勾股定理,以及等边三角形的判定与性质,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
把函数y=x2-4x+6的图象向左平移1个单位,再向上平移1个单位,所得图象对应的函数的解析式是( )
| A、y=(x-3)2+3 |
| B、y=(x-3)2+1 |
| C、y=(x-1)2+3 |
| D、y=(x-1)2+1 |
 A,B分别为河两岸的两点,其距离不能直接测出,请你根据所学的知识写出一个测量A,B两点之间距离的方法,要求:画出图形,写出已知和求证,并证明.
A,B分别为河两岸的两点,其距离不能直接测出,请你根据所学的知识写出一个测量A,B两点之间距离的方法,要求:画出图形,写出已知和求证,并证明. 一副三角板按如图所示放置,其中∠F=∠ACB=90°,∠E=30°,∠A=45°,点C在FD的延长线上,点B在DE上.
一副三角板按如图所示放置,其中∠F=∠ACB=90°,∠E=30°,∠A=45°,点C在FD的延长线上,点B在DE上. 已知数轴上一点A对应的数为4.
已知数轴上一点A对应的数为4. 如图,已知?ABCD中,过对角线的交点O的直线交CB,AD的延长线于E和F,证明:BE=DF.
如图,已知?ABCD中,过对角线的交点O的直线交CB,AD的延长线于E和F,证明:BE=DF.