题目内容
4.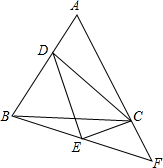 已知等腰三角形ABC,AB=AC,D为直线AB上一点,连接DC,以CD为斜边作直角三角形,并且∠DCE=∠BAC,连接BE并延长交AC的延长线于F.
已知等腰三角形ABC,AB=AC,D为直线AB上一点,连接DC,以CD为斜边作直角三角形,并且∠DCE=∠BAC,连接BE并延长交AC的延长线于F.(1)当tan∠BAC=$\sqrt{3}$时,求证:BE=EF;
(2)当tan∠BAC=$\frac{4}{3}$时,判断BE、EF的数量关系.
分析 (1)作△BDC的外接圆⊙O,延长CE交⊙O于点G,连接BG,如图,根据圆周角定理可得∠DBC=∠DGC,根据圆内接四边形的对角互补可得∠DBG+∠DCG=180°,结合条件∠DCE=∠BAC可证到BG∥AF,从而可得△BEG∽△FEC,则有$\frac{BE}{EF}$=$\frac{GE}{EC}$.要证BE=EF,只需证GE=EC.易证CD=CG,设EC=x,则DE=$\sqrt{3}$x,根据勾股定理可求出DC(CG),即可求出GE,问题得以解决;
(2)由tan∠BAC=$\frac{4}{3}$可得$\frac{DE}{EC}$=$\frac{4}{3}$,设EC=3k,则DE=4k,根据勾股定理可求出DC(CG),即可求出GE,结合$\frac{BE}{EF}$=$\frac{GE}{EC}$就可解决问题.
解答 解:(1)作△BDC的外接圆⊙O,延长CE交⊙O于点G,连接BG,如图,
则有∠DBC=∠DGC,∠DBG+∠DCG=180°.
∵∠DCE=∠BAC,∴∠DBG+∠BAC=180°,
∴BG∥AF,
∴△BEG∽△FEC,
∴$\frac{BE}{EF}$=$\frac{GE}{EC}$.
∵∠A+∠ABC+∠ACB=180°,∠DCG+∠DGC+∠GDC=180°,
∠DBC=∠DGC,∠BAC=∠DCG,
∴∠ACB=∠GDC.
∵AB=AC,∴∠ABC=∠ACB.
又∵∠ABC=∠DGC,
∴∠DGC=∠GDC,
∴CD=CG.
∵tan∠BAC=$\sqrt{3}$,tanDCE=$\frac{DE}{EC}$,∠BAC=∠DCE,
∴$\frac{DE}{EC}$=$\sqrt{3}$.
设EC=x,则DE=$\sqrt{3}$x,
∴CG=DC=2x,GE=GC-EC=x,
∴$\frac{BE}{EF}$=$\frac{GE}{EC}$=$\frac{x}{x}$=1,即BE=EF;
(2)∵tan∠BAC=$\frac{4}{3}$,tanDCE=$\frac{DE}{EC}$,∠BAC=∠DCE,
∴$\frac{DE}{EC}$=$\frac{4}{3}$.
设EC=3k,则DE=4k,
∴CG=DC=5k,GE=GC-EC=2k,
∴$\frac{BE}{EF}$=$\frac{GE}{EC}$=$\frac{2k}{3k}$=$\frac{2}{3}$,即3BE=2EF.
点评 本题主要考查了三角形的外接圆、圆周角定理、圆内接四边形的对角互补、平行线的判定与性质、相似三角形的判定与性质、等腰三角形的判定与性质、三角函数的定义、勾股定理等知识,构造辅助圆是解决本题的关键.

 天天向上口算本系列答案
天天向上口算本系列答案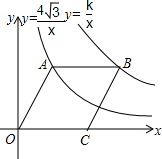 如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )
如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )| A. | 6$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 9$\sqrt{3}$ | D. | 12$\sqrt{3}$ |
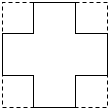 如图,将一块正方形铁片的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3.若设原铁片的边长为xcm,则根据题意可得关于x的方程(x-3×2)(x-3×2)×3=300.
如图,将一块正方形铁片的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3.若设原铁片的边长为xcm,则根据题意可得关于x的方程(x-3×2)(x-3×2)×3=300. 已知多项式A=(x+2)2+x(1-x)-9
已知多项式A=(x+2)2+x(1-x)-9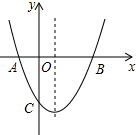 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,点P是抛物线上的一个动点,连接PA、PB,当S△PAB=8时,点P的坐标为(1+2$\sqrt{2}$,4)或(1-2$\sqrt{2}$,4)或(1,-4).
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,点P是抛物线上的一个动点,连接PA、PB,当S△PAB=8时,点P的坐标为(1+2$\sqrt{2}$,4)或(1-2$\sqrt{2}$,4)或(1,-4). 基础问题:
基础问题: