题目内容
16.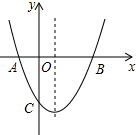 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,点P是抛物线上的一个动点,连接PA、PB,当S△PAB=8时,点P的坐标为(1+2$\sqrt{2}$,4)或(1-2$\sqrt{2}$,4)或(1,-4).
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,点P是抛物线上的一个动点,连接PA、PB,当S△PAB=8时,点P的坐标为(1+2$\sqrt{2}$,4)或(1-2$\sqrt{2}$,4)或(1,-4).
分析 根据待定系数法求出b,c的值,得出函数解析式,根据P点在抛物线上设出P点坐标,然后再由S△PAB=8,从而求出P点坐标.
解答 解:∵抛物线y=x2+bx+c与x轴的两个交点分别为A(-1,0),B(3,0)
∴OA=1,OB=3,$\left\{\begin{array}{l}{1-b+c=0}&{\;}\\{9+3b+c=0}&{\;}\end{array}\right.$,
解得:b=-2,c=-3,
∴抛物线的解析式为:y=x2-2x-3;
设点P的坐标为(x,y),∵AB=3+1=4,
∴S△PAB=$\frac{1}{2}$×4×|y|=8,
∴|y|=4,
∴y=±4,
当y=4时,x2-2x-3=4,
∴x1=1+2$\sqrt{2}$,x2=1-2$\sqrt{2}$,
当y=-4时,x2-2x-3=-4,
∴x=1,
∴当P点的坐标分别为(1+2$\sqrt{2}$,4)或(1-2$\sqrt{2}$,4)或(1,-4)时,S△PAB=8;
故答案为:(1+2$\sqrt{2}$,4)或(1-2$\sqrt{2}$,4)或(1,-4).
点评 本题考查用待定系数法求函数的解析式,抛物线与x轴的交点,函数图象点的坐标;熟练掌握用待定系数法求函数的解析式,把三角形面积公式同函数联系起来,是一种比较常见的题型.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
4.合肥市坚持以转变经济发展方式为主线,强化创新驱动,经济发展稳中有进,2015年前三季度,合肥市GDP超过3770亿元,3770亿用科学记数法可表示为( )
| A. | 3.77×103 | B. | 3.77×1010 | C. | 3.77×1011 | D. | 3.77×1012 |
11.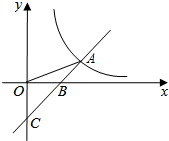 如图,直线y=x-b与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象在第一象限交于点A(3,1),连接OA,则△AOB的面积为( )
如图,直线y=x-b与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象在第一象限交于点A(3,1),连接OA,则△AOB的面积为( )
 如图,直线y=x-b与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象在第一象限交于点A(3,1),连接OA,则△AOB的面积为( )
如图,直线y=x-b与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象在第一象限交于点A(3,1),连接OA,则△AOB的面积为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
1. 如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA等于( )
如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA等于( )
 如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA等于( )
如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA等于( )| A. | 30° | B. | 36° | C. | 45° | D. | 32° |
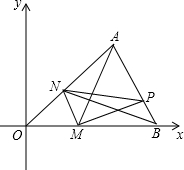 如图,在平面直角坐标中,△AOB的三个顶点的坐标分别是A(4,4),O(0,0),B(6,0),点M是射线OB上的一动点,过点M作MN∥AB,MN与射线OA交于点N,P是AB边上的任意点,连接AM,PM,PN,BN,设△PMN的面积为S.
如图,在平面直角坐标中,△AOB的三个顶点的坐标分别是A(4,4),O(0,0),B(6,0),点M是射线OB上的一动点,过点M作MN∥AB,MN与射线OA交于点N,P是AB边上的任意点,连接AM,PM,PN,BN,设△PMN的面积为S.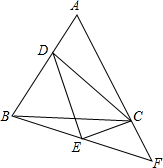 已知等腰三角形ABC,AB=AC,D为直线AB上一点,连接DC,以CD为斜边作直角三角形,并且∠DCE=∠BAC,连接BE并延长交AC的延长线于F.
已知等腰三角形ABC,AB=AC,D为直线AB上一点,连接DC,以CD为斜边作直角三角形,并且∠DCE=∠BAC,连接BE并延长交AC的延长线于F.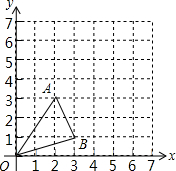 如图,在平面直角坐标系中,以原点O为位似中心,将△OAB放大到原来的2倍后得到△OA′B′,其中A、B在图中格点上,点A、B的对应点分别为A′、B′.
如图,在平面直角坐标系中,以原点O为位似中心,将△OAB放大到原来的2倍后得到△OA′B′,其中A、B在图中格点上,点A、B的对应点分别为A′、B′.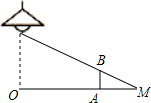 如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点0)20米的A处,则小明的影长为( )米.
如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点0)20米的A处,则小明的影长为( )米.