题目内容
16.关于x的方程$\frac{3x-a}{x+1}$=-2的解是负数,求a的取值范围.分析 先求出原方程的解,然后根据关于x的方程$\frac{3x-a}{x+1}$=-2的解是负数,可以求得a的取值范围,本题得以解决.
解答 解:$\frac{3x-a}{x+1}$=-2
方程两边同乘以x+1,得
3x-a=-2(x+1)
解得,x=$\frac{a-2}{5}$,
∵关于x的方程$\frac{3x-a}{x+1}$=-2的解是负数,
∴$\frac{a-2}{5}<0$,
∴a-2<0,
解得a<2,
即a的取值范围是a<2.
点评 本题考查分式方程的解,解题的关键是明确题意,会解分式方程,根据题目的要求会求a的取值范围.

练习册系列答案
相关题目
11.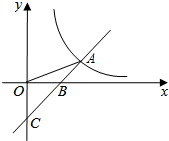 如图,直线y=x-b与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象在第一象限交于点A(3,1),连接OA,则△AOB的面积为( )
如图,直线y=x-b与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象在第一象限交于点A(3,1),连接OA,则△AOB的面积为( )
 如图,直线y=x-b与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象在第一象限交于点A(3,1),连接OA,则△AOB的面积为( )
如图,直线y=x-b与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象在第一象限交于点A(3,1),连接OA,则△AOB的面积为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
5.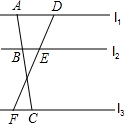 如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,已知AB=2,AC=5,DF=6,则DE的长是( )
如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,已知AB=2,AC=5,DF=6,则DE的长是( )
 如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,已知AB=2,AC=5,DF=6,则DE的长是( )
如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,已知AB=2,AC=5,DF=6,则DE的长是( )| A. | 3 | B. | $\frac{12}{5}$ | C. | $\frac{18}{5}$ | D. | $\frac{5}{2}$ |
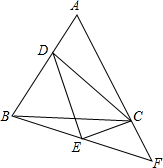 已知等腰三角形ABC,AB=AC,D为直线AB上一点,连接DC,以CD为斜边作直角三角形,并且∠DCE=∠BAC,连接BE并延长交AC的延长线于F.
已知等腰三角形ABC,AB=AC,D为直线AB上一点,连接DC,以CD为斜边作直角三角形,并且∠DCE=∠BAC,连接BE并延长交AC的延长线于F.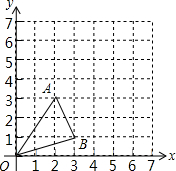 如图,在平面直角坐标系中,以原点O为位似中心,将△OAB放大到原来的2倍后得到△OA′B′,其中A、B在图中格点上,点A、B的对应点分别为A′、B′.
如图,在平面直角坐标系中,以原点O为位似中心,将△OAB放大到原来的2倍后得到△OA′B′,其中A、B在图中格点上,点A、B的对应点分别为A′、B′. 如图,为了计算河的宽度,某学习小组在河对岸选定一个目标点A,再在河岸的这一边选取点B和点C,使AB⊥BC,然后再选取点E,使E C⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=160 米,DC=80米,E C=49米,求A、B间的距离.
如图,为了计算河的宽度,某学习小组在河对岸选定一个目标点A,再在河岸的这一边选取点B和点C,使AB⊥BC,然后再选取点E,使E C⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=160 米,DC=80米,E C=49米,求A、B间的距离.