题目内容
9.在正数范围内定义一种运算△,其规则为a△b=$\frac{1}{a}$+$\frac{1}{b}$,求方程x△(x+2)=$\frac{6}{{x}^{2}+2x}$的解.分析 根据题中的新定义将所求式子化为普通运算,去分母转化为整式方程,求出方程的解得到x的值,代入检验即可得到原分式方程的解.
解答 解:根据题意,得:$\frac{1}{x}+\frac{1}{x+2}$=$\frac{6}{{x}^{2}+2x}$,
两边都乘以最简公分母x(x+2),得:x+2+x=6,
解得:x=2,
经检验x=2是原分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.弄清题中的新定义是解本题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目
4.合肥市坚持以转变经济发展方式为主线,强化创新驱动,经济发展稳中有进,2015年前三季度,合肥市GDP超过3770亿元,3770亿用科学记数法可表示为( )
| A. | 3.77×103 | B. | 3.77×1010 | C. | 3.77×1011 | D. | 3.77×1012 |
1. 如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA等于( )
如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA等于( )
 如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA等于( )
如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA等于( )| A. | 30° | B. | 36° | C. | 45° | D. | 32° |
19.下列语句不是命题的是( )
| A. | 两条直线相交,只有一个交点 | B. | 以点O为圆心、3cm长为半径画弧 | ||
| C. | 1+1<2 | D. | 等角的补角相等 |
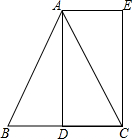 已知,如图,△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE;垂足为E.
已知,如图,△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE;垂足为E.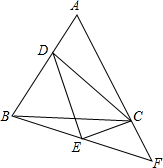 已知等腰三角形ABC,AB=AC,D为直线AB上一点,连接DC,以CD为斜边作直角三角形,并且∠DCE=∠BAC,连接BE并延长交AC的延长线于F.
已知等腰三角形ABC,AB=AC,D为直线AB上一点,连接DC,以CD为斜边作直角三角形,并且∠DCE=∠BAC,连接BE并延长交AC的延长线于F.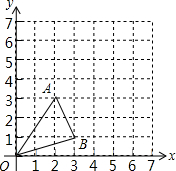 如图,在平面直角坐标系中,以原点O为位似中心,将△OAB放大到原来的2倍后得到△OA′B′,其中A、B在图中格点上,点A、B的对应点分别为A′、B′.
如图,在平面直角坐标系中,以原点O为位似中心,将△OAB放大到原来的2倍后得到△OA′B′,其中A、B在图中格点上,点A、B的对应点分别为A′、B′.