题目内容
20.先化简,再求值:($\frac{2}{a-1}+1$)÷$\frac{{a}^{2}+a}{{a}^{2}-2a+1}$,其中a=3.分析 先把括号内通分,再把分子分母因式分解,接着把除法运算化为乘法运算后约分得到原式=$\frac{a}{a-1}$,然后把a的值代入计算即可.
解答 解:原式=$\frac{2+a-1}{a-1}$•$\frac{(a-1)^{2}}{a(a+1)}$
=$\frac{a-1}{a}$,
当a=3 时,原式=$\frac{3-1}{3}$=$\frac{2}{3}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
10.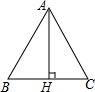 如图,等边△ABC的高AH等于$\sqrt{3}$,那么该三角形的面积为( )
如图,等边△ABC的高AH等于$\sqrt{3}$,那么该三角形的面积为( )
 如图,等边△ABC的高AH等于$\sqrt{3}$,那么该三角形的面积为( )
如图,等边△ABC的高AH等于$\sqrt{3}$,那么该三角形的面积为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
11.2022年将在北京-张家口举办冬季奥运会,很多学校开设了相关的课程.某校8名同学参加了冰壶选修课,他们被分成甲、乙两组进行训练,身高(单位:cm)如下表所示:
设两队队员身高的平均数依次为$\overline{{x}_{甲}}$,$\overline{{x}_{乙}}$,方差依次为S甲2,S乙2,下列关系中完全正确的是( )
| 队员1 | 队员2 | 队员3 | 队员4 | |
| 甲组 | 176 | 177 | 175 | 176 |
| 乙组 | 178 | 175 | 177 | 174 |
| A. | $\overline{{x}_{甲}}=\overline{{x}_{乙}}$,S甲2<S乙2 | B. | $\overline{{x}_{甲}}=\overline{{x}_{乙}}$,S甲2>S乙2 | ||
| C. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,S甲2<S乙2 | D. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,S甲2>S乙2 |
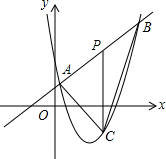 如图,直线y=x+4和抛物线y=ax2+bx+12(a≠0)相交于A(1,5)和B(8,n),点P是线段AB上异于A,B的动点,过点P作PC⊥x轴,交抛物线于点C.
如图,直线y=x+4和抛物线y=ax2+bx+12(a≠0)相交于A(1,5)和B(8,n),点P是线段AB上异于A,B的动点,过点P作PC⊥x轴,交抛物线于点C. 如图,在四边形ABCD中,AC⊥BD,EF∥AC∥HG,EH∥BD∥FG,求证:四边形EFGH是矩形.
如图,在四边形ABCD中,AC⊥BD,EF∥AC∥HG,EH∥BD∥FG,求证:四边形EFGH是矩形.