题目内容
5.先化简再求值:$\frac{{x}^{2}-4}{{x}^{2}+2x}÷(x-\frac{4x-4}{x})$,其中x是一元二次方程x2-4x-1=0的正数根.分析 先把括号内通分,再把分子分母因式分解,然后把除法运算化为乘法运算,约分得到原式=$\frac{1}{x-2}$,再利用配方法解方程x2-4x-1=0,把正数根代入计算即可.
解答 解:原式=$\frac{(x+2)(x-2)}{x(x+2)}$÷$\frac{{x}^{2}-(4x-4)}{x}$
=$\frac{(x+2)(x-2)}{x(x+2)}$•$\frac{x}{(x-2)^{2}}$
=$\frac{1}{x-2}$,
解x2-4x-1=0得x1=2+$\sqrt{5}$,x2=2-$\sqrt{5}$,
当x=2+$\sqrt{5}$时,原式=$\frac{1}{2+\sqrt{5}-2}$=$\frac{\sqrt{5}}{5}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
15. 实数a,b,c在数轴上的位置如图所示,则代数式|a+b|-|b-a|+|a-c|+c=( )
实数a,b,c在数轴上的位置如图所示,则代数式|a+b|-|b-a|+|a-c|+c=( )
 实数a,b,c在数轴上的位置如图所示,则代数式|a+b|-|b-a|+|a-c|+c=( )
实数a,b,c在数轴上的位置如图所示,则代数式|a+b|-|b-a|+|a-c|+c=( )| A. | -3a+2c | B. | -a-ab-2c | C. | a-2b | D. | 3a |
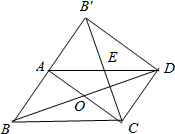 如图所示,在平行四边形ABCD纸片中,AC⊥AB,AC与BD相交于点O,将△ABC沿对角线AC翻折得到△AB′C,若四边形ABCD的面积为12cm2,则翻折后纸片重叠部分的面积是3cm2.
如图所示,在平行四边形ABCD纸片中,AC⊥AB,AC与BD相交于点O,将△ABC沿对角线AC翻折得到△AB′C,若四边形ABCD的面积为12cm2,则翻折后纸片重叠部分的面积是3cm2. 已知长度分别为3,6,2x-1的三条正整数长线段可以组成一个三角形.
已知长度分别为3,6,2x-1的三条正整数长线段可以组成一个三角形.