题目内容
15.解不等式组$\left\{\begin{array}{l}{2(x-2)≤3x-3}\\{\frac{x}{3}<\frac{x+1}{4}}\end{array}\right.$并写出它的所有非负整数解.分析 首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集,然后确定解集中的非负整数解即可.
解答 解:$\left\{\begin{array}{l}{2(x-2)≤3x-3…①}\\{\frac{x}{3}<\frac{x+1}{4}…②}\end{array}\right.$,
解①得x≥-1,
解②得x<3.
则不等式组的解集是-1≤x<3.
则不等式组的非负整数解是0,1,2.
点评 此题考查的是一元一次不等式组的解法.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
6.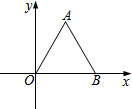 如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=4,则点A的坐标为( )
如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=4,则点A的坐标为( )
 如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=4,则点A的坐标为( )
如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=4,则点A的坐标为( )| A. | (2,$\sqrt{3}$) | B. | (2,4) | C. | (2,2$\sqrt{3}$) | D. | (2$\sqrt{3}$,2) |
10.我国央行公布的数据显示,中国2015年11月外汇储备为34383亿美元.34383亿用科学记数法可表示为( )
| A. | 34.383×1011 | B. | 3.4383×1012 | C. | 3.4383×1013 | D. | 3.4383×1011 |
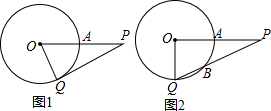 已知:P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.
已知:P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.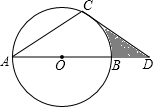 如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D=30°.
如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D=30°.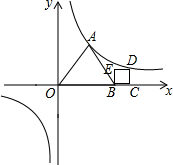 已知,反比例函数y=$\frac{\sqrt{3}}{x}$的图象上有两点A和D,且△OBA是等边三角形,四边形BCDE是正方形,则D点坐标(1+$\sqrt{\sqrt{3}+1}$,-1+$\sqrt{\sqrt{3}+1}$).
已知,反比例函数y=$\frac{\sqrt{3}}{x}$的图象上有两点A和D,且△OBA是等边三角形,四边形BCDE是正方形,则D点坐标(1+$\sqrt{\sqrt{3}+1}$,-1+$\sqrt{\sqrt{3}+1}$).