题目内容
 如图已知,?ABCD中,AE⊥BC于E,AE=BE=CE=m,且m是方程3x2-7x-6=0的一个正根,求?ABCD的周长.
如图已知,?ABCD中,AE⊥BC于E,AE=BE=CE=m,且m是方程3x2-7x-6=0的一个正根,求?ABCD的周长.考点:平行四边形的性质,解一元二次方程-因式分解法
专题:
分析:利用因式分解法解一元二次方程得到m的值,再求出BC,利用勾股定理列式求出AB,然后根据平行四边形的周长公式列式计算即可得解.
解答:解:3x2-7x-6=0,
(3x+2)(x-3)=0,
3x+2=0,x-3=0,
解得x1=-
,x2=3,
所以,AE=BE=CE=3,
所以,BC=BE+CE=3+3=6,
∵AE⊥BC,
∴由勾股定理得,AB=
=3
,
所以,?ABCD的周长=2(3
+6)=6
+12.
(3x+2)(x-3)=0,
3x+2=0,x-3=0,
解得x1=-
| 2 |
| 3 |
所以,AE=BE=CE=3,
所以,BC=BE+CE=3+3=6,
∵AE⊥BC,
∴由勾股定理得,AB=
| 32+32 |
| 2 |
所以,?ABCD的周长=2(3
| 2 |
| 2 |
点评:本题考查了平行四边形的性质,解一元二次方程,勾股定理,比较简单,解方程求出m的值是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
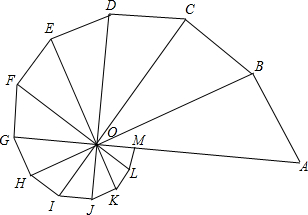 如图所示的图形是由12个有公共顶点O的直角三角形拼成的,∠AOB=∠BOC=…∠LOM=30°.你能从图中找出与△ABO位似的图形吗?它们的位似比是多少?
如图所示的图形是由12个有公共顶点O的直角三角形拼成的,∠AOB=∠BOC=…∠LOM=30°.你能从图中找出与△ABO位似的图形吗?它们的位似比是多少?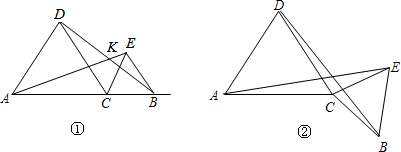
 如图,在⊙O中,BC、CD为⊙O的弦,过O作OA⊥BC交⊙O于点A,连接AD,若∠CDA=25°,∠AOB的度数是多少?
如图,在⊙O中,BC、CD为⊙O的弦,过O作OA⊥BC交⊙O于点A,连接AD,若∠CDA=25°,∠AOB的度数是多少?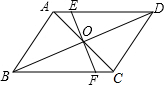 如图,点O为平行四边形ABCD的对角线BD的中点,EF过点O与AD、BC分别相交于点E、F.若B、D两点关于EF对称,请判断四边形EBFD为何种四边形?并说明你的理由.
如图,点O为平行四边形ABCD的对角线BD的中点,EF过点O与AD、BC分别相交于点E、F.若B、D两点关于EF对称,请判断四边形EBFD为何种四边形?并说明你的理由.