题目内容
已知
为正数,a+b=2,求
+
的最小值.
| a |
| b |
| a2+4 |
| b2+1 |
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:用a表示出b,从而得到
+
的最小值相当于点(a,0)到(0,2)和(2,1)的距离之和的最小值,然后确定出点(2,1)关于x轴的对称点(2,-1),再利用勾股定理列式计算即可得解.
| a2+4 |
| b2+1 |
解答: 解:∵a+b=2,
解:∵a+b=2,
∴b=2-a,
∴
+
=
+
,
∴
+
的最小值相当于点(a,0)到(0,2)和(2,1)的距离之和的最小值,
如图,点(2,1)关于x轴的对称点为(2,-1),
(0,2)和(2,-1)的距离为
=
,
所以,
+
的最小值为
.
 解:∵a+b=2,
解:∵a+b=2,∴b=2-a,
∴
| a2+4 |
| b2+1 |
| a2+4 |
| (2-a)2+1 |
∴
| a2+4 |
| b2+1 |
如图,点(2,1)关于x轴的对称点为(2,-1),
(0,2)和(2,-1)的距离为
| (2+1)2+22 |
| 13 |
所以,
| a2+4 |
| b2+1 |
| 13 |
点评:本题考查了轴对称确定最短路线问题,坐标与图形性质,难点在于考虑利用轴对称问题确定最小值,作出图形更形象直观.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 如图,正方形ABCD中,∠EAF=45°,BE=2,FC=6,求EF的长.
如图,正方形ABCD中,∠EAF=45°,BE=2,FC=6,求EF的长. 观察下图,图中有多少同位角、内错角、同旁内角?请把它们列出来.
观察下图,图中有多少同位角、内错角、同旁内角?请把它们列出来.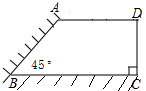 校园要建苗圃,其形状如直角梯形,有两边借用夹角为45°的两面墙,如图,另外两边是总长为30m的铁栅栏.
校园要建苗圃,其形状如直角梯形,有两边借用夹角为45°的两面墙,如图,另外两边是总长为30m的铁栅栏. 如图已知,?ABCD中,AE⊥BC于E,AE=BE=CE=m,且m是方程3x2-7x-6=0的一个正根,求?ABCD的周长.
如图已知,?ABCD中,AE⊥BC于E,AE=BE=CE=m,且m是方程3x2-7x-6=0的一个正根,求?ABCD的周长. 如图∠AOB=80°,OD是∠AOB的角平分线,∠AOC=3∠BOC,求∠COD的度数.
如图∠AOB=80°,OD是∠AOB的角平分线,∠AOC=3∠BOC,求∠COD的度数.