题目内容
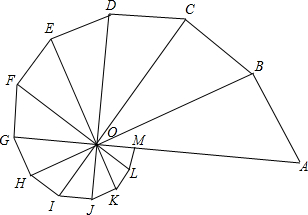 如图所示的图形是由12个有公共顶点O的直角三角形拼成的,∠AOB=∠BOC=…∠LOM=30°.你能从图中找出与△ABO位似的图形吗?它们的位似比是多少?
如图所示的图形是由12个有公共顶点O的直角三角形拼成的,∠AOB=∠BOC=…∠LOM=30°.你能从图中找出与△ABO位似的图形吗?它们的位似比是多少?考点:位似变换
专题:
分析:利用锐角三角函数关系进而求出LK=
,KJ=(
)2,JI=(
)3…,再求出位似比即可.
| 2 | ||
|
| 2 | ||
|
| 2 | ||
|
解答:解:设ML为1,
∵∠AOB=∠BOC=…∠LOM=30°,
∴LK=
,KJ=(
)2,JI=(
)3…
故第n个图形的边长为:(
)n-1,
故HG=(
)5,AB=(
)11,
∵△OGH与△OAB位似,则位似比为:(
)5:(
)11=
.
∵∠AOB=∠BOC=…∠LOM=30°,
∴LK=
| 2 | ||
|
| 2 | ||
|
| 2 | ||
|
故第n个图形的边长为:(
| 2 | ||
|
故HG=(
| 2 | ||
|
| 2 | ||
|
∵△OGH与△OAB位似,则位似比为:(
| 2 | ||
|
| 2 | ||
|
| 27 |
| 64 |
点评:此题主要考查了位似图形的性质以及锐角三角函数关系,得出边长变化规律是解题关键.

练习册系列答案
相关题目
下列运算正确的是( )
A、
| ||||||||||
B、3
| ||||||||||
C、
| ||||||||||
D、(
|
 如图,正方形ABCD中,∠EAF=45°,BE=2,FC=6,求EF的长.
如图,正方形ABCD中,∠EAF=45°,BE=2,FC=6,求EF的长.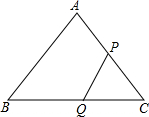 如图,在△ABC中,AB=AC=25cm,BC=30cm,点P从点C出发,沿CA以2.5cm/s的速度向点A运动.同时点Q从B点出发沿BC以4cm/s的速度向C运动,PQ中有一点到达终点时,两点同时停止运动,设运动时间为t.
如图,在△ABC中,AB=AC=25cm,BC=30cm,点P从点C出发,沿CA以2.5cm/s的速度向点A运动.同时点Q从B点出发沿BC以4cm/s的速度向C运动,PQ中有一点到达终点时,两点同时停止运动,设运动时间为t.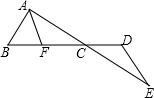 如图,AB=DE,AE、BD相交于点C,AF∥DE交BD于点F,∠B+∠D=180°.求证:CF=CD.
如图,AB=DE,AE、BD相交于点C,AF∥DE交BD于点F,∠B+∠D=180°.求证:CF=CD. 如图已知,?ABCD中,AE⊥BC于E,AE=BE=CE=m,且m是方程3x2-7x-6=0的一个正根,求?ABCD的周长.
如图已知,?ABCD中,AE⊥BC于E,AE=BE=CE=m,且m是方程3x2-7x-6=0的一个正根,求?ABCD的周长.