题目内容
 如图,在⊙O中,BC、CD为⊙O的弦,过O作OA⊥BC交⊙O于点A,连接AD,若∠CDA=25°,∠AOB的度数是多少?
如图,在⊙O中,BC、CD为⊙O的弦,过O作OA⊥BC交⊙O于点A,连接AD,若∠CDA=25°,∠AOB的度数是多少?考点:圆周角定理,垂径定理
专题:
分析:根据垂径定理求出弧AC=弧AB,求出弧的度数,即可求出圆心角的度数.
解答:解:∵OA为半径,OA⊥BC,
∴弧AC=弧AB,
∵∠CDA=25°,
∴弧AC和弧AB的度数都是50°,
∴∠AOB=50°.
∴弧AC=弧AB,
∵∠CDA=25°,
∴弧AC和弧AB的度数都是50°,
∴∠AOB=50°.
点评:本题考查了垂径定理,圆心角、弧、弦之间的关系的应用,解此题的关键是求出弧AB的度数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
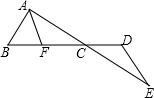 如图,AB=DE,AE、BD相交于点C,AF∥DE交BD于点F,∠B+∠D=180°.求证:CF=CD.
如图,AB=DE,AE、BD相交于点C,AF∥DE交BD于点F,∠B+∠D=180°.求证:CF=CD. 如图已知,?ABCD中,AE⊥BC于E,AE=BE=CE=m,且m是方程3x2-7x-6=0的一个正根,求?ABCD的周长.
如图已知,?ABCD中,AE⊥BC于E,AE=BE=CE=m,且m是方程3x2-7x-6=0的一个正根,求?ABCD的周长.