题目内容
6. 四边形ABCD为梯形其中AB∥CD,∠AEG=∠CEH,AF=CF,求证:四边形EGFH为平行四边形.
四边形ABCD为梯形其中AB∥CD,∠AEG=∠CEH,AF=CF,求证:四边形EGFH为平行四边形.
分析 欲证明四边形EGFH是平行四边形,只要证明∠FME=∠ENF,∠MFN=∠MEN.
解答 证明:∵AE=DE,∠AFB=∠DFN,
∴∠DAE=∠ADE,
∵AB∥CD,∠BAD+∠ADC=180°,
∴∠AED=∠BAM+∠NDC,
∵∠FBC+∠BFC+∠BCF=180°,
∵∠ABC+∠DCB=180°,
∴∠BFC=∠ABF+DCF,
∵∠AFB=∠DFC,
∴∠FAB+∠ABF=∠FCD+FDC,
∴∠MAB+∠MBA=∠NCD+∠NDC,
∴∠AMB=∠CND,
∴∠FME=∠ENF,
∵∠BFC=∠ABM+∠DCN,∠AED=∠ABM+∠NDC,∠AMB=∠CND,
∴∠ABM+∠DCN=∠BAM+∠NDC,
∴∠BFC=∠AED,
∴四边形FMEN为平行四边形.
点评 本题考查梯形的性质、平行四边形的判定、等腰三角形的性质等知识,解题的关键利用两组对角分别相等的四边形是平行四边形解决问题,属于中考常考题型.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
11.x,-2x2,4x3,-8x4…根据你发现的规律,写出第6个式子是( )
| A. | 16x5 | B. | 16x6 | C. | -32x6 | D. | 32x6 |
18. 如图是六边形ABCDEF,则该图形的对角线的条数是( )
如图是六边形ABCDEF,则该图形的对角线的条数是( )
 如图是六边形ABCDEF,则该图形的对角线的条数是( )
如图是六边形ABCDEF,则该图形的对角线的条数是( )| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
16.下列方程为一元二次方程的是( )
| A. | 3x2-2xy-5y2=0 | B. | x(x-3)=x2+5 | C. | x-$\frac{2}{x}$=8 | D. | x(x-2)=3 |
 纸片△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),若∠1=20°,则∠2的度数为60°.
纸片△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),若∠1=20°,则∠2的度数为60°. 如图,矩形ABCD中,CE平分∠BCD交AD于F,AE⊥CE于E,连BE交AD于N,连BD交CE于M,若CE=CB,则下列结论:①△AEF≌△CDF;②N为BE的黄金分割点;③S△MBC=(3+2$\sqrt{2}$)S△NEA;④BD=$\sqrt{2}$BE;其中正确结论个数是( )
如图,矩形ABCD中,CE平分∠BCD交AD于F,AE⊥CE于E,连BE交AD于N,连BD交CE于M,若CE=CB,则下列结论:①△AEF≌△CDF;②N为BE的黄金分割点;③S△MBC=(3+2$\sqrt{2}$)S△NEA;④BD=$\sqrt{2}$BE;其中正确结论个数是( )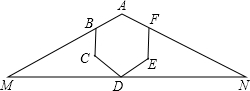 如图,等腰三角形AMN中放置了一个正六边形,已知三角形AMN的面积是160平方厘米,那么正六边形ABCDEF的面积是60平方厘米.
如图,等腰三角形AMN中放置了一个正六边形,已知三角形AMN的面积是160平方厘米,那么正六边形ABCDEF的面积是60平方厘米.