题目内容
19.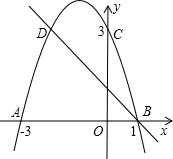 如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.(1)D点坐标(-2,3);
(2)求二次函数的解析式;
(3)若把二次函数向左平移2个单位,再向下平移3个单位,直接写出平移后的解析式;
(4)根据图象直接写出使一次函数值小于二次函数值的x的取值范围.
分析 (1)利用点C、D是二次函数图象上的一对对称点,可得出D点的坐标;
(2)设该抛物线的解析式为y=a(x+3)(x-1)(a≠0),然后将点C的坐标代入来求a的值;
(3)利用平移的特点直接写出抛物线解析式;
(4)在坐标系中利用x取相同值,比较出对应值的大小,从而确定,两函数的大小关系.
解答 解:(1)∵抛物线的对称轴是x=-1,而C、D关于直线x=-1对称,
∴D(-2,3);
故答案为:-2,3.
(2)设该抛物线的解析式为y=a(x+3)(x-1)(a≠0),
把C(0,3)代入,得
3=a(0+3)(0-1),
解得 a=-1,
所以该抛物线的解析式为y=-(x+3)(x-1)=-x2-2x+3,
即y=-x2-2x+3;
(3)由(2)知,抛物线的解析式为y=-x2-2x+3=-(x+1)2+4,
∵把二次函数向左平移2个单位,再向下平移3个单位,
∴平移后抛物线解析式为y=-(x+3)2+1=-x2-6x-8,
(4)根据图象知,一次函数值小于二次函数值的x的取值范围是:-2<x<1
点评 此题是二次函数综合题,主要考查了抛物线与x轴的交点,二次函数的对称性,以及待定系数法求二次函数解析式和利用自变量的取值范围确定函数值大小关系,题目难度不大,非常典型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.在直角三角形中,如果有一个角是30°,这个直角三角形的三边之比最有可能的是( )
| A. | 3:4:5 | B. | 1:1:$\sqrt{2}$ | C. | 5:12:13 | D. | 1:$\sqrt{3}$:2 |
11.x,-2x2,4x3,-8x4…根据你发现的规律,写出第6个式子是( )
| A. | 16x5 | B. | 16x6 | C. | -32x6 | D. | 32x6 |
9.下列说法中正确的是( )
| A. | 弦是直径 | B. | 弧是半圆 | ||
| C. | 半圆是圆中最长的弧 | D. | 直径是圆中最长的弦 |
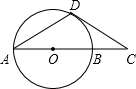 如图,AB是⊙O的直径,AD是⊙O的弦,过点D作⊙O的切线与AB的延长线交于点C,若∠CAD=30°,求证:AD=CD.
如图,AB是⊙O的直径,AD是⊙O的弦,过点D作⊙O的切线与AB的延长线交于点C,若∠CAD=30°,求证:AD=CD.
 如图,矩形ABCD中,CE平分∠BCD交AD于F,AE⊥CE于E,连BE交AD于N,连BD交CE于M,若CE=CB,则下列结论:①△AEF≌△CDF;②N为BE的黄金分割点;③S△MBC=(3+2$\sqrt{2}$)S△NEA;④BD=$\sqrt{2}$BE;其中正确结论个数是( )
如图,矩形ABCD中,CE平分∠BCD交AD于F,AE⊥CE于E,连BE交AD于N,连BD交CE于M,若CE=CB,则下列结论:①△AEF≌△CDF;②N为BE的黄金分割点;③S△MBC=(3+2$\sqrt{2}$)S△NEA;④BD=$\sqrt{2}$BE;其中正确结论个数是( )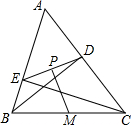 如图,BD和CE是△ABC的高,点M为BC的中点,连接DE,过点M作DE的垂线,垂足为点P.若PM=5,DE=6,tan∠DBC=$\frac{{\sqrt{2}}}{2}$,则CD的长为$\frac{2\sqrt{102}}{3}$.
如图,BD和CE是△ABC的高,点M为BC的中点,连接DE,过点M作DE的垂线,垂足为点P.若PM=5,DE=6,tan∠DBC=$\frac{{\sqrt{2}}}{2}$,则CD的长为$\frac{2\sqrt{102}}{3}$. 已知:如图,AB=AC,BD⊥AC于D,CE⊥AB于E.欲证明BD=CE,需证明△BDC≌△CEB,理由为
已知:如图,AB=AC,BD⊥AC于D,CE⊥AB于E.欲证明BD=CE,需证明△BDC≌△CEB,理由为