题目内容
9. 如图,在?ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=15cm2,则S△AOB等于60cm2.
如图,在?ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=15cm2,则S△AOB等于60cm2.
分析 利用平行四边形的性质得出AB=DC,AB∥CD,进而得出△DOE∽△BOA,再利用相似三角形的性质得出答案.
解答 解:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥CD,
∴△DOE∽△BOA,
∵E为CD中点,
∴$\frac{DE}{AB}$=$\frac{1}{2}$,
∴$\frac{{S}_{△DOE}}{{S}_{△BOA}}$=$\frac{1}{4}$,
∵S△DOE=15cm2,
∴S△AOB=60cm2.
故答案为:60.
点评 此题主要考查了平行四边形的性质以及相似三角形的判定与性质,得出△DOE∽△BOA是解题关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
4.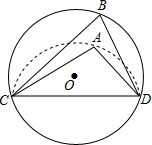 如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=100°,则∠B的度数是( )
如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=100°,则∠B的度数是( )
 如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=100°,则∠B的度数是( )
如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=100°,则∠B的度数是( )| A. | 100° | B. | 80° | C. | 60° | D. | 50° |
18. 如图是六边形ABCDEF,则该图形的对角线的条数是( )
如图是六边形ABCDEF,则该图形的对角线的条数是( )
 如图是六边形ABCDEF,则该图形的对角线的条数是( )
如图是六边形ABCDEF,则该图形的对角线的条数是( )| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
19.在某次聚会上,每两人都握了一次手,所有人共握手20次,设有x人参加这次聚会,下列列出方程正确的是( )
| A. | x(x-1)=20 | B. | $\frac{x(x-1)}{2}=20$ | C. | x(x+1)=20 | D. | $\frac{x(x+1)}{2}=20$ |
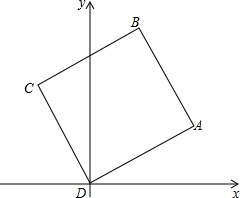 正方形ABCD如图放置,D与原点重合,C在第二象限,A点坐标为(8,4).
正方形ABCD如图放置,D与原点重合,C在第二象限,A点坐标为(8,4). 纸片△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),若∠1=20°,则∠2的度数为60°.
纸片△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),若∠1=20°,则∠2的度数为60°. 如图,矩形ABCD中,CE平分∠BCD交AD于F,AE⊥CE于E,连BE交AD于N,连BD交CE于M,若CE=CB,则下列结论:①△AEF≌△CDF;②N为BE的黄金分割点;③S△MBC=(3+2$\sqrt{2}$)S△NEA;④BD=$\sqrt{2}$BE;其中正确结论个数是( )
如图,矩形ABCD中,CE平分∠BCD交AD于F,AE⊥CE于E,连BE交AD于N,连BD交CE于M,若CE=CB,则下列结论:①△AEF≌△CDF;②N为BE的黄金分割点;③S△MBC=(3+2$\sqrt{2}$)S△NEA;④BD=$\sqrt{2}$BE;其中正确结论个数是( )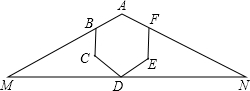 如图,等腰三角形AMN中放置了一个正六边形,已知三角形AMN的面积是160平方厘米,那么正六边形ABCDEF的面积是60平方厘米.
如图,等腰三角形AMN中放置了一个正六边形,已知三角形AMN的面积是160平方厘米,那么正六边形ABCDEF的面积是60平方厘米.