题目内容
5. 已知,如图,在△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=25°,则∠1的度数为105°.
已知,如图,在△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=25°,则∠1的度数为105°.
分析 先根据三角形的内角和定理可出∠C=180°-∠A-∠B=180°-65°-75°=40°;再根据折叠的性质得到∠C′=∠C=40°,再利用三角形的内角和定理以及外角性质得∠3+∠2+∠5+∠C′=180°,∠5=∠4+∠C=∠4+40°,即可得到∠3+∠4=65°,然后利用平角的定义即可求出∠1.
解答 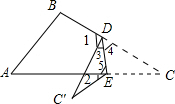 解:如图,
解:如图,
∵∠A=65°,∠B=75°,
∴∠C=180°-∠A-∠B=180°-65°-75°=40°;
又∵将三角形纸片的一角折叠,使点C落在△ABC外,
∴∠C′=∠C=40°,
而∠3+∠2+∠5+∠C′=180°,∠5=∠4+∠C=∠4+40°,∠2=25°,
∴∠3+25°+∠4+40°+40°=180°,
∴∠3+∠4=75°,
∴∠1=180°-75°=105°.
故答案为:105°.
点评 本题考查了折叠前后两图形全等,即对应角相等,对应线段相等.也考查了三角形的内角和定理以及外角性质.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
10.在直角三角形中,如果有一个角是30°,这个直角三角形的三边之比最有可能的是( )
| A. | 3:4:5 | B. | 1:1:$\sqrt{2}$ | C. | 5:12:13 | D. | 1:$\sqrt{3}$:2 |
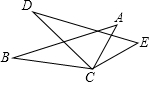 如图,已知∠B=∠D,AB=DE,要推得△ABC≌△EDC;
如图,已知∠B=∠D,AB=DE,要推得△ABC≌△EDC; 纸片△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),若∠1=20°,则∠2的度数为60°.
纸片△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),若∠1=20°,则∠2的度数为60°. 如图,矩形ABCD中,CE平分∠BCD交AD于F,AE⊥CE于E,连BE交AD于N,连BD交CE于M,若CE=CB,则下列结论:①△AEF≌△CDF;②N为BE的黄金分割点;③S△MBC=(3+2$\sqrt{2}$)S△NEA;④BD=$\sqrt{2}$BE;其中正确结论个数是( )
如图,矩形ABCD中,CE平分∠BCD交AD于F,AE⊥CE于E,连BE交AD于N,连BD交CE于M,若CE=CB,则下列结论:①△AEF≌△CDF;②N为BE的黄金分割点;③S△MBC=(3+2$\sqrt{2}$)S△NEA;④BD=$\sqrt{2}$BE;其中正确结论个数是( )