题目内容
观察下列等式:
=1-
,
=
-
,
=
-
.
将以上三个等式两边分别相加得:
+
+
=1-
+
-
+
-
=1-
=
(1)猜想并写出
=
(2)直接写出下列各式的计算结果:
①
+
+
+…+
= ;
②
+
+
+…+
= ;
(3)探究并计算:
+
+
+…+
.
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
将以上三个等式两边分别相加得:
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
(1)猜想并写出
| 1 |
| n(n+1) |
(2)直接写出下列各式的计算结果:
①
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2013×2014 |
②
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
(3)探究并计算:
| 1 |
| 2×4 |
| 1 |
| 4×6 |
| 1 |
| 6×8 |
| 1 |
| 2012×2014 |
考点:规律型:数字的变化类
专题:
分析:(1)分母是两个连续自然数的乘积,分子是1,可以拆成分子是1,分母是两个自然数的分数的差;
(2)①②把分数拆分,进一步抵消得出答案即可;
(3)提取
,进一步利用上面的规律拆分抵消得出答案即可.
(2)①②把分数拆分,进一步抵消得出答案即可;
(3)提取
| 1 |
| 4 |
解答:解:(1)
=
-
;
(2)直接写出下列各式的计算结果:
①
+
+
+…+
=
;
②
+
+
+…+
=
;
(3)
+
+
+…+
=
×(1-
+
-
+
-
+…+
-
)
=
×(1-
)
=
×
=
.
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
(2)直接写出下列各式的计算结果:
①
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2013×2014 |
| 2013 |
| 2014 |
②
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
| n |
| n+1 |
(3)
| 1 |
| 2×4 |
| 1 |
| 4×6 |
| 1 |
| 6×8 |
| 1 |
| 2012×2014 |
=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 1006 |
| 1 |
| 1007 |
=
| 1 |
| 4 |
| 1 |
| 1007 |
=
| 1 |
| 4 |
| 1006 |
| 1007 |
=
| 503 |
| 2014 |
点评:此题考查数字的变化规律,找出数字之间的运算规律:分母是两个连续自然数的乘积,分子是1,可以拆成分子是1,分母是两个自然数的分数的差,进一步利用规律,解决问题.

练习册系列答案
相关题目
 如图,已知∠1=∠2,AD=AB,求证:△ABC≌△ADC.
如图,已知∠1=∠2,AD=AB,求证:△ABC≌△ADC.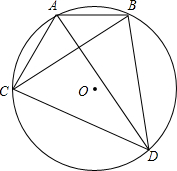 如图,AD,BC是圆O的两条相互垂直的弦,AB=2,CD=4,则⊙O的半径为
如图,AD,BC是圆O的两条相互垂直的弦,AB=2,CD=4,则⊙O的半径为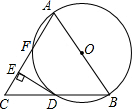 AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使BD=DC,连AC,过D作DE⊥AC于E,AC交⊙O于F.求证:
AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使BD=DC,连AC,过D作DE⊥AC于E,AC交⊙O于F.求证: 如图,正方形ABCD的边长为a cm,剪去4个角后成为正八边形,则正八边形的边长为多少?面积为多少?
如图,正方形ABCD的边长为a cm,剪去4个角后成为正八边形,则正八边形的边长为多少?面积为多少?