题目内容
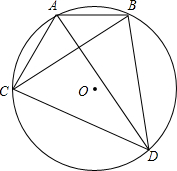如图，AD，BC是圆O的两条相互垂直的弦，AB=2，CD=4，则⊙O的半径为考点：垂径定理,勾股定理
专题：
分析：如图，作辅助线；证明DE=AB=2；求出CE=2
，即可解决问题．
| 5 |
解答：
解：连接CO并延长，交⊙O于点E；连接BE、DE；
则∠CBE=∠CDE=90°；
∵BC⊥AD，
∴AD∥BE，
∴
=
，
∴DE=AB=2；
由勾股定理得：
CE2=CD2+DE2，而CD=4，
∴CE=2
，
∴⊙O的半径为
，
故答案为
．
解：连接CO并延长，交⊙O于点E；连接BE、DE；则∠CBE=∠CDE=90°；
∵BC⊥AD，
∴AD∥BE，
∴
 |
| AB |
|
| DE |
∴DE=AB=2；
由勾股定理得：
CE2=CD2+DE2，而CD=4，
∴CE=2
| 5 |
∴⊙O的半径为
| 5 |
故答案为
| 5 |
点评：该题主要考查了垂径定理及其应用问题；解题的关键是作辅助线；灵活运用圆周角定理及其推论、勾股定理等几何知识点来分析、解答．
练习册系列答案
互动英语系列答案
相关题目
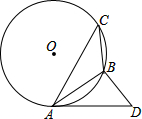已知AB为⊙O的弦，C为⊙O上一点，∠C=∠BAD，且BD⊥AB于点B，
小明在用图象法解二元一次方程组时所画图象如图，那么这个方程组的解是
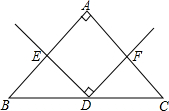已知：∠A=90°，AB=AC，D是BC的中点，∠EDF=90°．求证：DE=DF．