题目内容
5.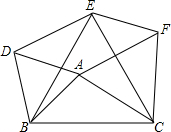 如图,把△ABC绕点B逆时针旋转60°到△DBE的位置,再将△ABC绕点C顺时针旋转60°到△FEC的位置,顺次连接A、F、E、D得到四边形AFED.
如图,把△ABC绕点B逆时针旋转60°到△DBE的位置,再将△ABC绕点C顺时针旋转60°到△FEC的位置,顺次连接A、F、E、D得到四边形AFED.(1)试判断四边形AFED是何种特殊的四边形,并证明你的结论;
(2)当△ABC满足一定条件时,四边形AFED能成为正方形吗?如果能,请直接写出需满足的条件;如果不能,请说明理由.
分析 (1)由旋转的性质可知,∠ACF=60°,CA=CF,则△ACF为等边三角形,可得AC=AF,由旋转的性质可知AC=DE,故DE=AF,同理可证AD=EF,故四边形AFED是平行四边形;
(2)根据正方形的判定可知,有一个角是直角且有一组邻边相等的平行四边形是正方形.由(1)可知∠CAF=∠BAD=60°,当四边形AFED是正方形时,∠DAF=90°,且AD=AF,则∠BAC=360°-60°-60°-90°=150°,AB=AC.
解答  解:(1)∵将△ABC绕点C顺时针旋转60°到△FEC的位置,
解:(1)∵将△ABC绕点C顺时针旋转60°到△FEC的位置,
∴∠ACF=60°,CA=CF,
∴△ACF为等边三角形,AC=AF,
又∵把△ABC绕点B逆时针旋转60°到△DBE的位置,
∴AC=DE,
∴DE=AF,
同理可证AD=EF,
∴四边形AFED是平行四边形;
(2)当∠BAC=150°,且AB=AC时,四边形AFED能成为正方形.
点评 本题考查了正方形的判定,旋转的性质,平行四边形的判定.关键是由旋转的性质推出等边三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
. 已知:如图,点E,C在线段BF上,AB=DE,AB∥DE,BE=CF.求证:AC=DF.
已知:如图,点E,C在线段BF上,AB=DE,AB∥DE,BE=CF.求证:AC=DF.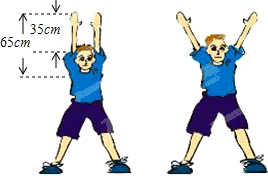 一位同学的手臂长65cm,当他竖直举高双臂时,指尖高出头顶35cm.当他的手臂与水平方向成60°时,他的指尖高出头顶多少厘米(精确到0.1cm)
一位同学的手臂长65cm,当他竖直举高双臂时,指尖高出头顶35cm.当他的手臂与水平方向成60°时,他的指尖高出头顶多少厘米(精确到0.1cm)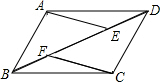 如图,在?ABCD中,点E、F在BD上,且BF=DE,
如图,在?ABCD中,点E、F在BD上,且BF=DE,