题目内容
16. 已知:如图,点E,C在线段BF上,AB=DE,AB∥DE,BE=CF.求证:AC=DF.
已知:如图,点E,C在线段BF上,AB=DE,AB∥DE,BE=CF.求证:AC=DF.
分析 由AB∥DE,根据两直线平行,同位角相等,即可求得∠B=∠DEF,由BE=CF,可得BC=EF,然后根据SAS即可判定△ABC≌△DEF,根据全等三角形的对应边相等,即可证得AC=DF.
解答 证明:∵AB∥DE,
∴∠B=∠DEF,
∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
$\left\{\begin{array}{l}{AB=DE}\\{∠B=∠DEF}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△DEF(SAS),
∴AC=DF.
点评 本题考查了全等三角形的判定与性质与平行线的性质.熟练掌握全等三角形的判定与性质是解决问题的关键.

练习册系列答案
相关题目
1.要使代数式$\frac{1}{1+\frac{1}{x+1}}$有意义,则必须( )
| A. | x≠-1或x≠-2 | B. | x≠-1 | C. | x≠-2 | D. | x≠-1且x≠-2 |
8.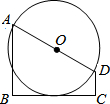 如图,BC是以AD为直径的⊙O的切线,AB⊥BC,DC⊥BC.在下列哪种情况下,四边形ABCD的面积是整数( )
如图,BC是以AD为直径的⊙O的切线,AB⊥BC,DC⊥BC.在下列哪种情况下,四边形ABCD的面积是整数( )
 如图,BC是以AD为直径的⊙O的切线,AB⊥BC,DC⊥BC.在下列哪种情况下,四边形ABCD的面积是整数( )
如图,BC是以AD为直径的⊙O的切线,AB⊥BC,DC⊥BC.在下列哪种情况下,四边形ABCD的面积是整数( )| A. | AB=9,CD=4 | B. | AB=7,CD=3 | C. | AB=5,CD=2 | D. | AB=3,CD=1 |
6. 如图所示的物体是一个几何体,其俯视图是( )
如图所示的物体是一个几何体,其俯视图是( )
 如图所示的物体是一个几何体,其俯视图是( )
如图所示的物体是一个几何体,其俯视图是( )| A. |  | B. |  | C. |  | D. |  |
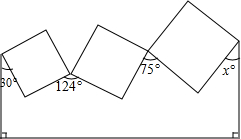 如图,三个正方形一些顶点标出了角的度数,则x=41.
如图,三个正方形一些顶点标出了角的度数,则x=41.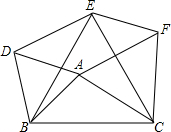 如图,把△ABC绕点B逆时针旋转60°到△DBE的位置,再将△ABC绕点C顺时针旋转60°到△FEC的位置,顺次连接A、F、E、D得到四边形AFED.
如图,把△ABC绕点B逆时针旋转60°到△DBE的位置,再将△ABC绕点C顺时针旋转60°到△FEC的位置,顺次连接A、F、E、D得到四边形AFED.