题目内容
13.反比例函数y=$\frac{a}{x}$的图象经过点(-$\sqrt{3}$,$\sqrt{3}$),则a的值为-3.分析 直接把点(-$\sqrt{3}$,$\sqrt{3}$)代入反比例函数y=$\frac{a}{x}$,求出a的值即可.
解答 解:∵反比例函数y=$\frac{a}{x}$的图象经过点(-$\sqrt{3}$,$\sqrt{3}$),
∴a=$\sqrt{3}$•(-$\sqrt{3}$)=-3.
故答案为:-3.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
1.要使代数式$\frac{1}{1+\frac{1}{x+1}}$有意义,则必须( )
| A. | x≠-1或x≠-2 | B. | x≠-1 | C. | x≠-2 | D. | x≠-1且x≠-2 |
8.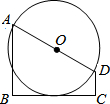 如图,BC是以AD为直径的⊙O的切线,AB⊥BC,DC⊥BC.在下列哪种情况下,四边形ABCD的面积是整数( )
如图,BC是以AD为直径的⊙O的切线,AB⊥BC,DC⊥BC.在下列哪种情况下,四边形ABCD的面积是整数( )
 如图,BC是以AD为直径的⊙O的切线,AB⊥BC,DC⊥BC.在下列哪种情况下,四边形ABCD的面积是整数( )
如图,BC是以AD为直径的⊙O的切线,AB⊥BC,DC⊥BC.在下列哪种情况下,四边形ABCD的面积是整数( )| A. | AB=9,CD=4 | B. | AB=7,CD=3 | C. | AB=5,CD=2 | D. | AB=3,CD=1 |
18.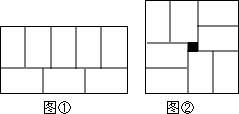 用8块相同的长方形地砖拼矩形,小明拼成了图①,小红拼成了图②,小红所拼图形中间刚好多出一个边长为1的小正方形,则每个小长方形的长宽分别为( )
用8块相同的长方形地砖拼矩形,小明拼成了图①,小红拼成了图②,小红所拼图形中间刚好多出一个边长为1的小正方形,则每个小长方形的长宽分别为( )
 用8块相同的长方形地砖拼矩形,小明拼成了图①,小红拼成了图②,小红所拼图形中间刚好多出一个边长为1的小正方形,则每个小长方形的长宽分别为( )
用8块相同的长方形地砖拼矩形,小明拼成了图①,小红拼成了图②,小红所拼图形中间刚好多出一个边长为1的小正方形,则每个小长方形的长宽分别为( )| A. | 10,6 | B. | 15,9 | C. | 5,3 | D. | 20,12 |
2.已知实数a、b满足a2=2-2a,b2=2-2b,则$\frac{b}{{a}^{2}}$+$\frac{a}{{b}^{2}}$=( )
| A. | 5 | B. | 1±$\sqrt{3}$ | C. | 5或1-$\sqrt{3}$ | D. | 5或1±$\sqrt{3}$ |
3.下列计算中正确的是( )
| A. | 3a+2a=a5 | B. | (3ab2)3=9a3b6 | C. | a2•a3=a6 | D. | (-a3)2=a6 |
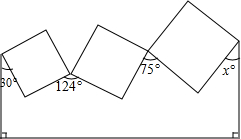 如图,三个正方形一些顶点标出了角的度数,则x=41.
如图,三个正方形一些顶点标出了角的度数,则x=41.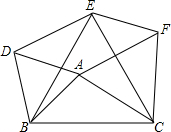 如图,把△ABC绕点B逆时针旋转60°到△DBE的位置,再将△ABC绕点C顺时针旋转60°到△FEC的位置,顺次连接A、F、E、D得到四边形AFED.
如图,把△ABC绕点B逆时针旋转60°到△DBE的位置,再将△ABC绕点C顺时针旋转60°到△FEC的位置,顺次连接A、F、E、D得到四边形AFED.