题目内容
10. 如图,在△A1B1C1中,已知A1B1=7,B1C1=4,A1C1=6,依次连接△A1B1C1三边中点,得△A2B2C2,再依次连接△A2B2C2的三边中点,得△A3B3C3,…,则△AnBnCn的周长=$\frac{17}{{2}^{n-1}}$.
如图,在△A1B1C1中,已知A1B1=7,B1C1=4,A1C1=6,依次连接△A1B1C1三边中点,得△A2B2C2,再依次连接△A2B2C2的三边中点,得△A3B3C3,…,则△AnBnCn的周长=$\frac{17}{{2}^{n-1}}$.
分析 根据三角形的中位线平行于第三边并且等于第三边的一半可得中点三角形的周长等于原三角形的周长的一半,然后写出前三个三角形的周长,再根据指数的变化规律写出△AnBnCn的周长即可.
解答 解:∵A1B1=7,B1C1=4,A1C1=6,
∴△A1B1C1的周长=7+4+6=17,
∵依次连接△A1B1C1三边中点,得△A2B2C2,
∴△A2B2C2的周长=$\frac{1}{2}$×17,
∵再依次连接△A2B2C2的三边中点,得△A3B3C3,
∴△A3B3C3的周长=$\frac{1}{2}$×($\frac{1}{2}$×17)=$\frac{1}{{2}^{2}}$×17,
…,
△AnBnCn的周长=$\frac{1}{{2}^{n-1}}$×17=$\frac{17}{{2}^{n-1}}$.
故答案为:$\frac{17}{{2}^{n-1}}$.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,三角形的周长,熟记定理并明确中点三角形的周长等于原三角形的周长的一半是解题的关键.

练习册系列答案
相关题目
20.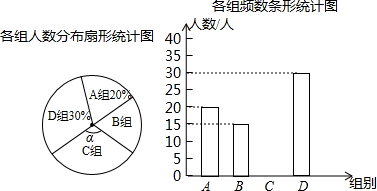 小强同学对本校学生完成家庭作业的时间进行了随机抽样调查,并绘成如下不完整的三个统计图表.
小强同学对本校学生完成家庭作业的时间进行了随机抽样调查,并绘成如下不完整的三个统计图表.
各组频数、频率统计表
(1)a=0.15,b=100,∠α=126,并将条形统计图补充完整.
(2)若该校有学生3200人,估计完成家庭作业时间超过1小时的人数.
(3)根据以上信息,请您给校长提一条合理的建议.
 小强同学对本校学生完成家庭作业的时间进行了随机抽样调查,并绘成如下不完整的三个统计图表.
小强同学对本校学生完成家庭作业的时间进行了随机抽样调查,并绘成如下不完整的三个统计图表.各组频数、频率统计表
| 组别 | 时间(小时) | 频数(人) | 频率 |
| A | 0≤x≤0.5 | 20 | 0.2 |
| B | 0.5<x≤1 | 15 | a |
| C | 1<x≤1.5 | 35 | 0.35 |
| D | x>1.5 | 30 | 0.3 |
| 合计 | b | 1.0 | |
(2)若该校有学生3200人,估计完成家庭作业时间超过1小时的人数.
(3)根据以上信息,请您给校长提一条合理的建议.
5.在四边形ABCD中,对角线AC、BD相交于点O,下列说法正确的是( )
| A. | 如果AB=BC,AC⊥BD,那么四边形ABCD是菱形 | |
| B. | 如果AC=BD,AC⊥BD,那么四边形ABCD是菱形 | |
| C. | 如果AB=BC,AD∥BC,那么四边形ABCD是平行四边形 | |
| D. | 如果AO=CO,BO=DO,BC=CD,那么四边形ABCD是菱形 |
2.下列运算正确的是( )
| A. | (-x-2)(x-2)=x2-4 | B. | 2x(x2-2x-3)=2x3-4x2-6x | ||
| C. | (x-2y)2=x2-4xy+2y2 | D. | (x-1)(x+4)=x2-4 |
19. 如图,A、B两点在数轴上表示的数分别是a、b,则下列式子中一定成立的是( )
如图,A、B两点在数轴上表示的数分别是a、b,则下列式子中一定成立的是( )
 如图,A、B两点在数轴上表示的数分别是a、b,则下列式子中一定成立的是( )
如图,A、B两点在数轴上表示的数分别是a、b,则下列式子中一定成立的是( )| A. | ab<2a | B. | 1-3a<1-3b | C. | |a|-|b|>0 | D. | ab>-b |
 如图,O是直线AB上一点,∠AOC=∠BOD,射线OE平分∠BOC,∠EOD=42°,求∠EOC的大小.
如图,O是直线AB上一点,∠AOC=∠BOD,射线OE平分∠BOC,∠EOD=42°,求∠EOC的大小.