题目内容
1.某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料,生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克,经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产B产品不少于38件,问符合生产条件的生产方案有哪几种?
分析 (1)设甲材料每千克x元,乙材料每千克y元,根据购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元,可列出方程组,解方程组即可求得;
(2)设生产A产品m件,生产B产品(60-m)件,根据用于购买甲、乙两种材料的资金不超过9900元,且生产B产品不少于38件即可列不等式求得m的范围,然后确定正整数解即可确定方案.
解答 解:(1)解:(1)设甲材料每千克x元,乙材料每千克y元,
则$\left\{\begin{array}{l}{x+y=60}\\{2x+3y=155}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=25}\\{y=35}\end{array}\right.$,
所以甲材料每千克25元,乙材料每千克35元;
(2)设生产A产品m件,生产B产品(60-m)件,则生产这60件产品的材料费为
25×4m+35×1m+25×3(60-m)+35×3(60-m)=-45m+10800,
由题意:-45m+10800≤9900,解得m≥20,
又∵60-m≥38,解得m≤22,
∴20≤m≤22,
∴m的值为20,21,22,
共有三种方案:
①生产A产品20件,生产B产品40件;
②生产A产品21件,生产B产品39件;
③生产A产品22件,生产B产品38件.
点评 本题考查了一次函数的应用:通过实际问题列出一次函数关系式,然后根据一次函数的性质解决问题.也考查了二元一次方程组以及一元一次不等式组的应用.

练习册系列答案
相关题目
9.?ABCD中,对角线AC、BD相交于点O,则下列结论中错误的是( )
| A. | AB=CD | B. | AC=BD | C. | AD=CB | D. | AO=OC |
11.据国家财政部估算,初步预计2009年全国财政收入将为65720亿元,用科学记数法表示为( )
| A. | 6.572×1010 | B. | 6.572×1011 | C. | 6.572×1012 | D. | 6.572×1013 |
 操作题
操作题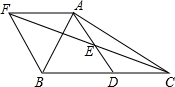 如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.
如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF. 如图,在△A1B1C1中,已知A1B1=7,B1C1=4,A1C1=6,依次连接△A1B1C1三边中点,得△A2B2C2,再依次连接△A2B2C2的三边中点,得△A3B3C3,…,则△AnBnCn的周长=$\frac{17}{{2}^{n-1}}$.
如图,在△A1B1C1中,已知A1B1=7,B1C1=4,A1C1=6,依次连接△A1B1C1三边中点,得△A2B2C2,再依次连接△A2B2C2的三边中点,得△A3B3C3,…,则△AnBnCn的周长=$\frac{17}{{2}^{n-1}}$.