题目内容
2.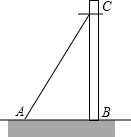 如图,要从电线杆离地面的C处向地面A处拉一条长10m的电缆,测得∠CAB=60°,则电线杆的高度BC是5$\sqrt{3}$m.
如图,要从电线杆离地面的C处向地面A处拉一条长10m的电缆,测得∠CAB=60°,则电线杆的高度BC是5$\sqrt{3}$m.
分析 首先根据直角三角形两锐角互余可得∠ACB=30°,再根据直角三角形30°角所对的直角边等于斜边的一半可得AB=$\frac{1}{2}$AC,然后利用勾股定理计算出BC的长即可.
解答 解:∵∠CAB=60°,CB⊥AB,
∴∠ACB=30°,
∴AB=$\frac{1}{2}$AC,
∵AC=10m,
∴AB=5m,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{100-25}$=5$\sqrt{3}$(m),
故答案为:5$\sqrt{3}$m.
点评 此题主要考查了勾股定理的应用,关键是掌握直角三角形的性质.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
13.若方程组$\left\{\begin{array}{l}{4x+3y=5}\\{kx+(1-k)y=8}\end{array}\right.$的解中,x的值比y的值的相反数大1,则k的值为( )
| A. | 3 | B. | -3 | C. | 2 | D. | 无答案 |
11.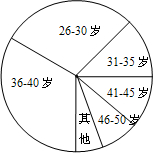 2012年3月全国两会在北京召开,公众最关心哪些问题?九一班学生就老百姓最关注的两会热点问题,在网络上发布了相应的调查问卷,到目前为止,共有不同年龄段的2880人参与,其中31~35岁关心问题的具体情况统计如下:
2012年3月全国两会在北京召开,公众最关心哪些问题?九一班学生就老百姓最关注的两会热点问题,在网络上发布了相应的调查问卷,到目前为止,共有不同年龄段的2880人参与,其中31~35岁关心问题的具体情况统计如下:
(1)请将统计表中遗漏的数据补上;
(2)求扇形图(如图)中表示31~35岁的扇形的圆心角的度数;
(3)在参加调查的31~35岁段中随机抽取一人,关心物价调控或医疗改革的概率是多少?
 2012年3月全国两会在北京召开,公众最关心哪些问题?九一班学生就老百姓最关注的两会热点问题,在网络上发布了相应的调查问卷,到目前为止,共有不同年龄段的2880人参与,其中31~35岁关心问题的具体情况统计如下:
2012年3月全国两会在北京召开,公众最关心哪些问题?九一班学生就老百姓最关注的两会热点问题,在网络上发布了相应的调查问卷,到目前为止,共有不同年龄段的2880人参与,其中31~35岁关心问题的具体情况统计如下:| 关心问题 | 频数 | 频率 |
| 收入分配 | 90 | 0.25 |
| 住房问题 | 54 | 0.15 |
| 物价调控 | 36 | 0.1 |
| 医疗改革 | 18 | 0.05 |
| 养老保险 | 54 | 0.15 |
| 其他 | 108 | 0.30 |
| 合计 | 360 | 1 |
(2)求扇形图(如图)中表示31~35岁的扇形的圆心角的度数;
(3)在参加调查的31~35岁段中随机抽取一人,关心物价调控或医疗改革的概率是多少?

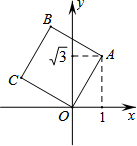 如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,$\sqrt{3}$),则(1)OA的长为2,(2)点C的坐标为(-$\sqrt{3}$,1).
如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,$\sqrt{3}$),则(1)OA的长为2,(2)点C的坐标为(-$\sqrt{3}$,1).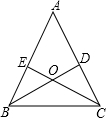 已知:如图,锐角△ABC的两条高BD、CE相交于点O,且BE=CD.
已知:如图,锐角△ABC的两条高BD、CE相交于点O,且BE=CD.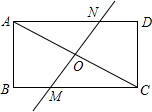 如图,将矩形ABCD沿直线MN对折,使A、C重合,直线MN交AC于O,且AB=6,BC=8
如图,将矩形ABCD沿直线MN对折,使A、C重合,直线MN交AC于O,且AB=6,BC=8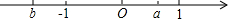 实数a、b在数轴上的位置如图所示,写出不等式组$\left\{\begin{array}{l}x+a>0\\ x-b>0\end{array}$的解集为x>-a.
实数a、b在数轴上的位置如图所示,写出不等式组$\left\{\begin{array}{l}x+a>0\\ x-b>0\end{array}$的解集为x>-a.