题目内容
7.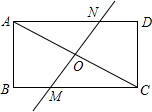 如图,将矩形ABCD沿直线MN对折,使A、C重合,直线MN交AC于O,且AB=6,BC=8
如图,将矩形ABCD沿直线MN对折,使A、C重合,直线MN交AC于O,且AB=6,BC=8(1)求证:△COM∽△CBA;
(2)求线段OM的长度.
分析 (1)由翻折的性质可知AB⊥MN,然后根据有两组角对应相等的两个三角形相似进行证明即可;
(2)先求得AC的长,由翻折的性质可知OC=$\frac{1}{2}AC$,然后利用相似三角形的性质进行求解即可.
解答 解:(1)由翻折的性质可知:AC⊥MN,
∴∠MOC=∠B=90°.
又∵∠OCM=∠BCA,
∴△COM∽△CBA.
(2)在Rt△ABC中,由勾股定理得AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10.
由翻折的性质可知:OC=$\frac{1}{2}AC$=5.
∵△COM∽△CBA,
∴$\frac{OM}{AB}=\frac{OC}{BC}$,即$\frac{OM}{6}=\frac{5}{8}$.
解得:OM=$\frac{15}{4}$.
点评 本题主要考查的是翻折变换、相似三角形的判定和性质、勾股定理,掌握翻折的性质是解题的关键.

练习册系列答案
相关题目
12. 如图,在梯形ABCD中,AD∥BC,AB=DC,BC-AD=AB,过D作DE∥AB交BC于E,则△DEC是( )
如图,在梯形ABCD中,AD∥BC,AB=DC,BC-AD=AB,过D作DE∥AB交BC于E,则△DEC是( )
 如图,在梯形ABCD中,AD∥BC,AB=DC,BC-AD=AB,过D作DE∥AB交BC于E,则△DEC是( )
如图,在梯形ABCD中,AD∥BC,AB=DC,BC-AD=AB,过D作DE∥AB交BC于E,则△DEC是( )| A. | 不等边三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
19.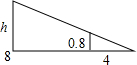 如图,小伟在打网球时,击球点距离球网的水平距离是8米.已知网高是0.8米,要使球恰好能打过网,且落在离网4米的位置,则球拍击打的高度h为( )
如图,小伟在打网球时,击球点距离球网的水平距离是8米.已知网高是0.8米,要使球恰好能打过网,且落在离网4米的位置,则球拍击打的高度h为( )
 如图,小伟在打网球时,击球点距离球网的水平距离是8米.已知网高是0.8米,要使球恰好能打过网,且落在离网4米的位置,则球拍击打的高度h为( )
如图,小伟在打网球时,击球点距离球网的水平距离是8米.已知网高是0.8米,要使球恰好能打过网,且落在离网4米的位置,则球拍击打的高度h为( )| A. | 1.0 | B. | 1.6 | C. | 2.0 | D. | 2.4 |
16. 如图是一个正方体的展开图,将它折叠成正方体后,“我”字的对面是( )
如图是一个正方体的展开图,将它折叠成正方体后,“我”字的对面是( )
 如图是一个正方体的展开图,将它折叠成正方体后,“我”字的对面是( )
如图是一个正方体的展开图,将它折叠成正方体后,“我”字的对面是( )| A. | 校 | B. | 东 | C. | 母 | D. | 中 |
17.一项工程,甲独做要x天完成,乙独做要y天完成,则甲、乙合做完成工程需要的天数为( )
| A. | x+y | B. | $\frac{x+y}{2}$ | C. | $\frac{xy}{x+y}$ | D. | $\frac{x+y}{xy}$ |
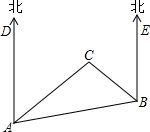 如图,C岛在A岛的北偏东55°方向,B岛在A岛的北偏东85°方向,C岛在B岛的北偏西40°方向,从C岛看A、B两岛的视角∠ACB是多少度?
如图,C岛在A岛的北偏东55°方向,B岛在A岛的北偏东85°方向,C岛在B岛的北偏西40°方向,从C岛看A、B两岛的视角∠ACB是多少度? 如图,在矩形ABCD中,AB=6cm,BC=10cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,当一个点到达终点时,另一个点立即停止移动,点P运动时间为t秒.
如图,在矩形ABCD中,AB=6cm,BC=10cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,当一个点到达终点时,另一个点立即停止移动,点P运动时间为t秒.
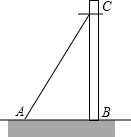 如图,要从电线杆离地面的C处向地面A处拉一条长10m的电缆,测得∠CAB=60°,则电线杆的高度BC是5$\sqrt{3}$m.
如图,要从电线杆离地面的C处向地面A处拉一条长10m的电缆,测得∠CAB=60°,则电线杆的高度BC是5$\sqrt{3}$m.