题目内容
10.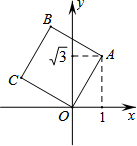 如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,$\sqrt{3}$),则(1)OA的长为2,(2)点C的坐标为(-$\sqrt{3}$,1).
如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,$\sqrt{3}$),则(1)OA的长为2,(2)点C的坐标为(-$\sqrt{3}$,1).
分析 (1)利用勾股定理直接计算即可求出OA的长;
(2)过点A作AD⊥x轴于D,过点C作CE⊥x轴于E,根据同角的余角相等求出∠OAD=∠COE,再利用“角角边”证明△AOD和△OCE全等,根据全等三角形对应边相等可得OE=AD,CE=OD,然后根据点C在第二象限写出坐标即可.
解答 解:(1)∵点A的坐标为(1,$\sqrt{3}$),
∴OA=$\sqrt{3+1}$=2,
故答案为:2;
(2)如图,过点A作AD⊥x轴于D,过点C作CE⊥x轴于E,
∵四边形OABC是正方形,
∴OA=OC,∠AOC=90°,
∴∠COE+∠AOD=90°,
又∵∠OAD+∠AOD=90°,
∴∠OAD=∠COE,
在△AOD和△OCE中,
$\left\{\begin{array}{l}{∠OAD=∠COE}\\{∠ADO=∠OEC=90°}\\{OA=OC}\end{array}\right.$,
∴△AOD≌△OCE(AAS),
∴OE=AD=$\sqrt{3}$,CE=OD=1,
∵点C在第二象限,
∴点C的坐标为(-$\sqrt{3}$,1).
故答案为(-$\sqrt{3}$,1).
点评 本题考查了全等三角形的判定与性质,正方形的性质,坐标与图形性质,作辅助线构造出全等三角形是解题的关键,也是本题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 如图,△ABC中,∠ACB=70°,将△ABC绕点B按逆时针方向旋转得到△BDE(点D与点A是对应点,点E与点C是对应点),且边DE恰好经过点C,则∠ABD的度数为( )
如图,△ABC中,∠ACB=70°,将△ABC绕点B按逆时针方向旋转得到△BDE(点D与点A是对应点,点E与点C是对应点),且边DE恰好经过点C,则∠ABD的度数为( )
 如图,△ABC中,∠ACB=70°,将△ABC绕点B按逆时针方向旋转得到△BDE(点D与点A是对应点,点E与点C是对应点),且边DE恰好经过点C,则∠ABD的度数为( )
如图,△ABC中,∠ACB=70°,将△ABC绕点B按逆时针方向旋转得到△BDE(点D与点A是对应点,点E与点C是对应点),且边DE恰好经过点C,则∠ABD的度数为( )| A. | 30° | B. | 40° | C. | 45° | D. | 50° |
19.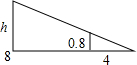 如图,小伟在打网球时,击球点距离球网的水平距离是8米.已知网高是0.8米,要使球恰好能打过网,且落在离网4米的位置,则球拍击打的高度h为( )
如图,小伟在打网球时,击球点距离球网的水平距离是8米.已知网高是0.8米,要使球恰好能打过网,且落在离网4米的位置,则球拍击打的高度h为( )
 如图,小伟在打网球时,击球点距离球网的水平距离是8米.已知网高是0.8米,要使球恰好能打过网,且落在离网4米的位置,则球拍击打的高度h为( )
如图,小伟在打网球时,击球点距离球网的水平距离是8米.已知网高是0.8米,要使球恰好能打过网,且落在离网4米的位置,则球拍击打的高度h为( )| A. | 1.0 | B. | 1.6 | C. | 2.0 | D. | 2.4 |
20.用甲乙两种原料配制成某种饮料,已知每千克的这两种原料的维生素C含量及购买这两种原料的价格如表所示:现配制这种饮料10kg,要求至少含有4200单位的维生素C,且购买原料的费用不超过72元.设所需甲种原料x(kg),则可列不等式组为( )
| 原料 | 甲 | 乙 |
| 维生素 | 600单位 | 100单位 |
| 原料价格 | 8元 | 4元 |
| A. | $\left\{\begin{array}{l}{600x+100x≥4200}\\{8(10-x)+4(10-x)≤72}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{600x+100(10-x)≥4200}\\{8x+4(10-x)≤72}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{600x+100x>4200}\\{8(10-x)+4(10-x)<72}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{600x+100x<4200}\\{8(10-x)+4(10-x)>72}\end{array}\right.$ |
 图中的两个三角形有几对相等的角?这两个三角形全等吗?请说明理由.
图中的两个三角形有几对相等的角?这两个三角形全等吗?请说明理由. 如图,在矩形ABCD中,AB=6cm,BC=10cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,当一个点到达终点时,另一个点立即停止移动,点P运动时间为t秒.
如图,在矩形ABCD中,AB=6cm,BC=10cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,当一个点到达终点时,另一个点立即停止移动,点P运动时间为t秒.
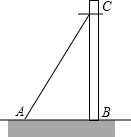 如图,要从电线杆离地面的C处向地面A处拉一条长10m的电缆,测得∠CAB=60°,则电线杆的高度BC是5$\sqrt{3}$m.
如图,要从电线杆离地面的C处向地面A处拉一条长10m的电缆,测得∠CAB=60°,则电线杆的高度BC是5$\sqrt{3}$m.